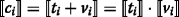- Research
- Open access
- Published:
An efficient privacy-preserving comparison protocol in smart metering systems
EURASIP Journal on Information Security volume 2016, Article number: 11 (2016)
Abstract
In smart grids, providing power consumption statistics to the customers and generating recommendations for managing electrical devices are considered to be effective methods that can help to reduce energy consumption. Unfortunately, providing power consumption statistics and generating recommendations rely on highly privacy-sensitive smart meter consumption data. From the past experience, we see that it is essential to find scientific solutions that enable the utility providers to provide such services for their customers without damaging customers’ privacy. One effective approach relies on cryptography, where sensitive data is only given in the encrypted form to the utility provider and is processed under encryption without leaking content. The proposed solutions using this approach are very effective for privacy protection but very expensive in terms of computation and communication. In this paper, we focus on an essential operation for designing a privacy-preserving recommender system for smart grids, namely comparison, that takes two encrypted values and outputs which one is greater than the other one. We improve the state-of-the-art comparison protocol based on Homomorphic Encryption in terms of computation and communication by 56 and 25 %, respectively, by introducing algorithmic changes and data packing. As the smart meters are very limited devices, the overall improvement achieved is promising for the future deployment of such cryptographic protocols for enabling privacy enhanced services in smart grids.
1 Introduction
Smart grids, as the next generation of power grid, are utilizing both communication technologies and information processing to monitor and manage power grids to enhance reliability, efficiency, and sustainability of power generation. One of the advantages of smart grids compared to traditional power grids is the ability to observe the power consumption of households in very short time intervals in the order of seconds to minutes. As a result of the fine-coarse data reporting, it is possible to provide power consumption statistics to the consumers, which might help to reduce the overall consumption by changing customer behavior, as pointed out in several works [1–5]. For example, Honebein et al. [6] defined people as the only true smart part of a smart grid; therefore, monitoring, understanding, and promoting the end-users’ roles from passive to active is considered as a fundamental action in smart grids. To this end, there are already several utility companies providing their customers devices and smart phone applications to monitor their real-time consumption. Furthermore, one of the goals of the utility providers, balancing the supply and the demand, also known as demand response (DR), can be achieved more effectively if the utility provider can also provide statistics about the power usage in the surrounding area and generate personalized recommendations, for example, to manage electrical devices like electric cars, heating systems, and ovens in the household [7].
Providing statistics on power consumption and generating personalized recommendations to inform customers are heavily dependent on the smart meter consumption readings. Unfortunately, these readings are highly privacy-sensitive [8–10]. The utility provider can use the readings from the smart meters for other purposes, misuse them or even transfer them to other entities without the consent of the customers. As seen in many cases, privacy is considered to be a big challenge for using smart meters to the fullest extent, e.g., enabling personalized services such as generating recommendations.
In this paper, we assume that the utility provider generates statistics and recommendations for the customers so that the customers can adjust the electrical devices for the most cost-effective and environmentally friendly manner. To achieve this, we rely on cryptography, which provides us tools to create privacy by design algorithms. For instance, there are already a number of studies for computing bills and aggregating data [11–14]. The main idea in this research line is to provide only the encrypted power consumption to the utility provider and enable processing the encrypted data without decrypting any sensitive information. This way, the utility provider cannot access to the content but at the same time can perform the algorithms required for the service. Unfortunately, the cryptographic algorithms for this purpose are expensive in terms of computation and communication, which mostly require smart meters to be involved in the computation [15–18]. Since the smart meters are very limited devices, improving the efficiency of the cryptographic algorithms is a challenge.
We address the efficiency problem of a fundamental operation, namely comparison, which is required to design any recommender system. In our setting, the encrypted consumption readings are collected from the customers by an aggregator and the utility provider has the decryption key. For privacy reasons, the aggregator cannot transfer the data directly to the utility provider but can co-operate with the utility provider to generate recommendations. One important step in the system is to compare values, which are only available in the encrypted form. More precisely, the aggregator has two encrypted values, and it needs to know which one is greater than the other one without revealing their contents to anyone including itself.
There are numerous comparison protocols designed for comparing encrypted values [15, 16, 18]. In this paper, we improve the state-of-the-art comparison protocol that relies on homomorphic encryption in terms of run-time by 56 % by introducing algorithmic changes. Furthermore, we also reduce communication cost of the protocol by 25 % by deploying data packing [19, 20]. Together, these improvements increase the overall efficiency of the comparison protocol with encrypted inputs, bringing smart meters one step closer to run privacy-preserving cryptographic protocols based on homomorphic encryption.
Note that a secure comparison protocol with encrypted values is needed in many applications, not only for generating recommendations, like face recognition [17], finger-code authentication [21], and K-means clustering [22]. Therefore, the protocol we improved in this paper provide a significant performance improvement for other applications as well.
2 Preliminaries
In this section, we describe the application setting, the security assumptions, and the cryptographic tools used in this work. We also present the symbols and their descriptions in Table 1.
2.1 Application setting
In our application setting, we define three roles: (1) smart meters installed at the households, (2) a data aggregator, and (3) a utility provider. Smart meters measure, encrypt, and send consumers’ power consumption to the data aggregator, which collects and analyzes encrypted power consumption. Then, the utility provider generates recommendations for its customers by running a cryptographic protocol with the data aggregator. The output of the cryptographic protocol, which depends on the purpose of the recommender system, is in the encrypted form; thus, it is not available neither to the data aggregator nor to the utility provider. The output is then revealed to the customer by using another protocol, secure decryption, which is explained in [23].
2.2 Security model
The proposed protocol in this work is built on the semi-honest adversarial model, where the data aggregator and the utility provider are honest in the sense that they faithfully follow the designed protocol but will try to infer information from the protocol execution transcript. This assumption is realistic since companies are expected to properly perform required services mentioned in the service level agreement, when engaging in a collaboration. We assume that the utility provider is the only party holding the private keys, while the smart meters and the data aggregator have the public keys for the encryption schemes. We assume that neither party colludes.
2.3 Homomorphic encryption
In this work, we rely on two additively homomorphic cryptosystems, Paillier [24] and Damgård, Geislet and Krøigaard (DGK) [15]. An additively homomorphic encryption scheme preserves certain structure that can be exploited to process ciphertexts without decryption. Given \(\mathcal {E}_{pk}(m_{1})\) and \(\mathcal {E}_{pk}(m_{2})\), a new ciphertext whose decryption yields the sum of the plaintext messages m 1 and m 2 can be obtained by performing a certain operation over the ciphertexts: \(\mathcal {D}_{sk}(\mathcal {E}_{pk}(m_{1}))\otimes (\mathcal {E}_{pk}(m_{2})) = m_{1}+m_{2}\).
Consequently, exponentiation of any ciphertext with a public value yields the encrypted product of the original plaintext and the exponent: \(\mathcal {D}_{sk}\left (\mathcal {E}_{pk}(m)^{e}\right) = e \cdot m\).
2.4 Paillier cryptosystem
The Paillier encryption function for a given message \(m\in \mathbb {Z}_{\eta }\) is defined as follows:
where η is the product of two distinct large prime numbers p and q, ciphertext \(c \in \mathbb {Z}^{*}_{\eta ^{2}}\), \(\tau \in _{R} \mathbb {Z}^{*}_{\eta }\) and g is a generator of order η. The decryption function is,
where λ η is the Carmichael value that is the smallest positive integer such that \(\phantom {\dot {i}\!}\{\forall a \in \mathbb {Z}^{*}_{\eta }\) : \(\phantom {\dot {i}\!}a^{\lambda _{\eta }}\equiv 1\:(\text {mod} \: \eta)\)} and \(L_{\eta }(x)= \frac {x-1}{\eta }\). The public key is (g,η) and the private key is λ η .
The homomorphic property can be shown as below:
2.5 DGK cryptosystem
We also use the DGK cryptosystem [15, 25], which is used in constructing cryptographic protocols [17, 23] for its efficiency due to its small message size. For generating the public and the private keys, there are three parameters: k, t, and ℓ, where ℓ<t<k. The process of key generation is as follows:
-
1.
Choose two distinct t-bit prime numbers v p , v q .
-
2.
Construct two distinct prime numbers p and q, where v p |(p−1) and v q |(q−1) such that n=p q is a k-bit RSA modulus.
-
3.
Choose u, the smallest possible prime number but greater than ℓ+2.
-
4.
Choose a random r that is a 2.5t-bit integer [15].
-
5.
Choose g and h such that ord(g)=u v p v q and ord(h)=v p v q .
The public and the private keys are p k=(n,g,h,u) and s k=(p,q,v p ,v q ), respectively. The encryption of a plaintext \(m \in \mathbb {Z}_{u} \) is given as follows:
To decrypt the ciphertext, one can build a look-up table for all \(m\in \mathbb {Z}_{u}\) values and obtain m from \(\phantom {\dot {i}\!}c^{v_{p}} \: \text {mod} \: p = (g^{v_{p}})^{m} \: \text {mod} \: p\). However, DGK scheme can efficiently check whether a ciphertext is an encryption of zero or not. To achieve this, we check whether \(\phantom {\dot {i}\!}c^{{v_{p}}{v_{q}}} \: \text {mod} \: n=1\) or more efficiently we only need to prove that \(\phantom {\dot {i}\!}c^{{v_{p}}{v_{q}}} \: \text {mod} \: p=1\) or \(\phantom {\dot {i}\!}c^{{v_{p}}{v_{q}}} \: \text {mod} \: q=1\), since u<p.
In the rest of the paper, we denote the ciphertext of a message m by [m] for the Paillier cryptosystem and  for the DGK.
for the DGK.
3 Secure comparison protocol with secret inputs
In this section, we describe the state-of-the-art secure comparison protocol (SCP), which takes two encrypted inputs and outputs the greater one in the encrypted form. SCP based on the DGK construction introduced in [25] is one of the widely-used comparison protocols due to its efficiency. The DGK comparison protocol is a sub-protocol in the SCP, where each party possesses a secret but plaintext value. The sub-protocol also uses the DGK cryptosystem for efficiency reasons.
The comparison protocol in [25] is modified and used by Erkin et al. in [17], and Veugen proposed an improved DGK comparison protocol (IDCP) in [18]. In the following, we describe the SCP construction.
For the sake of simplicity, we use the names Alice and Bob as the data aggregator and the utility provider, respectively. We assume that Bob has the secret key sk and Alice has access to two encrypted values, [a] and [b], and wants to know if a<b.
Initially, Alice computes [ z]=[2ℓ+a−b]=[2ℓ]·[a]·[b]−1 and then obtains the result of comparison as follows:
where [ z ℓ ] is the most significant bit of [ z] and the result of comparison. If z ℓ =1 then we have a>b, and otherwise a<b. A more efficient method of computing [ z ℓ ] is based on the IDCP, where we can compute z ℓ =⌊z/2ℓ⌋ and [a<b]=[ 1−z ℓ ]=[ 1]·[z ℓ ]−1, but we still need to compute [z mod 2ℓ]. A more detailed explanation regarding computation of [ z ℓ ] is provided in the following sections.
3.1 Computing [z mod 2ℓ]
Notice that Alice has access only to [ z], and interaction with Bob, who has the private key, is needed to compute modulo reduction, [zmod2ℓ]. However, Alice cannot give [ z] directly to Bob since this value reveals information on the difference of a and b. Therefore, Alice masks [ z] using a random value as follows:
where r is a (κ+ℓ)-bit uniformly random number and κ is a security parameter. After masking, Alice sends [ d] to Bob to perform modulo reduction, where Bob first decrypts [ d], then computes \(\acute {d}=d\ \text {mod}\ 2^{\ell }\) and sends \([\!\acute {d}]\) and [ d/2ℓ] back to Alice. Subsequently, to obtain [ zmod2ℓ], Alice computes \([\tilde {z}\text {mod}2^{\ell }]=[\!\acute {d}- r\text {mod}2^{\ell }]=[\!\acute {d}]\cdot [r \text {mod}2^{\ell }]^{-1}.\)
Note that z mod 2ℓ = \(\tilde {z}\ \text {mod}\ 2^{\ell }\) if \(\acute {d}>r\text {mod}2^{\ell }\). When \(\acute {d}<r\text {mod}2^{\ell }\), an underflow occurs, and Alice has to add 2ℓ to \([\!\tilde {z}]\) to make the value positive again. Therefore, Alice needs to determine whether \(\acute {d}>r\, \text {mod}\, 2^{\ell }\) or not. This is achieved by computing an encrypted value, [ λ], which shows the relation between \(\acute {d}\) and r mod2ℓ. Then, Alice can perform following computation to obtain [zmod2ℓ]:
Alice can obtain [ z ℓ ] by using Eq. 5. [ z ℓ ] can be computed more efficiently as follow:
where Ψ(x)=⌊x/2ℓ⌋. For computing [ λ], we run a secure comparison protocol with private inputs as described in the following section.
3.2 Computing [λ]
This protocol outputs an encrypted bit, which shows whether \(\acute {d} >\hat {r}=r\text {mod}2^{\ell }\) or not. However, different than the original problem of comparing encrypted a and b, in this protocol Alice and Bob possess \(\hat {r}\) and \(\acute {d}\) in plaintext, respectively. Based on this setting, the IDCP for computing [ λ] securely works as follows:
-
1.
Bob sends a bitwise encryption of his input,
 , to Alice.
, to Alice. -
2.
Alice chooses uniformly random bit δ, where δ∈{0,1}. Then she computes s=1−2·δ and
 as follows,
as follows, (9)
(9)where
 , and i=0,…,ℓ−1.
, and i=0,…,ℓ−1. -
3.
Alice blinds each
 with a uniformly random \(h_{i} \in _{R} \mathbb {Z}^{*}_{u}\) such that
with a uniformly random \(h_{i} \in _{R} \mathbb {Z}^{*}_{u}\) such that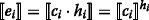 (10)
(10)then permutes
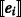 and sends them to Bob. Note that if c
t
=0, where t∈{0,…,ℓ−1} then e
t
=0 as well.
and sends them to Bob. Note that if c
t
=0, where t∈{0,…,ℓ−1} then e
t
=0 as well. -
4.
Bob checks whether there is a zero among
 values. If none of the
values. If none of the  values are encrypted zero then he sets \(\tilde {\lambda }=0\), otherwise \(\tilde {\lambda }=1\). Then he encrypts \(\tilde {\lambda }\) and sends \([\!\tilde {\lambda }]\) to Alice.
values are encrypted zero then he sets \(\tilde {\lambda }=0\), otherwise \(\tilde {\lambda }=1\). Then he encrypts \(\tilde {\lambda }\) and sends \([\!\tilde {\lambda }]\) to Alice. -
5.
Alice corrects \([\!\tilde {\lambda }]\) to obtain [ λ] as follows:
\([\!\lambda ]= \begin {cases} [\!\tilde {\lambda }] & \text {if}\ s=1 \\ [\!1]\cdot [\!\tilde {\lambda }]^{-1} & \text {if}\ s=-1 \end {cases}\)
After obtaining [ λ], Alice computes [z mod 2ℓ] and [z ℓ ] based on Eqs. 7 and 5 respectively.
4 Efficient privacy-preserving comparison protocol
In this section, we describe a new version of the original SCP based on the DGK construction, which is significantly more efficient in terms of run-time and communication cost.
4.1 Proposed comparison protocol
Complexity analysis and experimental results reveal that the XOR operation in computing  , in Eq. 9, has a significant impact on the overall efficiency of the DGK comparison protocol for the following two reasons:
, in Eq. 9, has a significant impact on the overall efficiency of the DGK comparison protocol for the following two reasons:
-
1.
Computing XOR is computationally expensive, since
 . Veugen [18] proposed a more efficient technique of computing XOR, where
. Veugen [18] proposed a more efficient technique of computing XOR, where  when \(\hat {r} =0\); otherwise,
when \(\hat {r} =0\); otherwise, 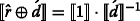 (recall that Alice and Bob have access to values \(\hat {r}\) and \( \acute {d}\), respectively and Alice is computing XOR). Thus, if \(\hat {r}\) equals to 1, one multiplication and one exponentiation with negative exponent should be computed over DGK ciphertexts, which affects the performance of DGK comparison protocol significantly.
(recall that Alice and Bob have access to values \(\hat {r}\) and \( \acute {d}\), respectively and Alice is computing XOR). Thus, if \(\hat {r}\) equals to 1, one multiplication and one exponentiation with negative exponent should be computed over DGK ciphertexts, which affects the performance of DGK comparison protocol significantly. -
2.
Since the equation that involves XOR is computed during the protocol with encrypted inputs, it is not possible to introduce pre-computation for
 to obtain a more efficient protocol.
to obtain a more efficient protocol.
Table 2 shows that computing  constitutes 70 % of the overall run-time of the IDCP for Alice.
constitutes 70 % of the overall run-time of the IDCP for Alice.
Based on these two facts, we propose a more efficient way of computing  , which does not rely on the original XOR computation. The value
, which does not rely on the original XOR computation. The value  can be re-written as follows:
can be re-written as follows:

Alice computes Eq. 11 in three steps:
-
1.
Bob computes
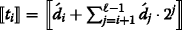 , and sends
, and sends 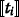 to Alice.
to Alice. -
2.
Alice computes
 .
. -
3.
Alice computes
 as follows,
as follows,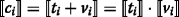 (12)
(12)
Note that Alice can pre-compute  and factor “3” is not needed in the computation of
and factor “3” is not needed in the computation of  . After computing all
. After computing all  values, Alice masks each
values, Alice masks each  and sends masked values to Bob, where he checks if any of the given masked
and sends masked values to Bob, where he checks if any of the given masked  is zero, then generates \([\tilde {\lambda }]\), and sends it to Alice. She corrects \([\tilde {\lambda }]\) based on value s to obtain [λ], computes Eq. 7, and 5 to obtain [z
ℓ
] as in the original protocol. Note that we compare \(2\acute {d}\) and \(2\hat {r}\) instead of \(\acute {d}\) and \(\hat {r}\) respectively for technical reasons explained in the following section.
is zero, then generates \([\tilde {\lambda }]\), and sends it to Alice. She corrects \([\tilde {\lambda }]\) based on value s to obtain [λ], computes Eq. 7, and 5 to obtain [z
ℓ
] as in the original protocol. Note that we compare \(2\acute {d}\) and \(2\hat {r}\) instead of \(\acute {d}\) and \(\hat {r}\) respectively for technical reasons explained in the following section.
4.1.1 4.1.1 Correctness proof of computing 
In this section, we prove the correctness of generating  by Eq. 12. In order to do that, we check if Eq. 12 generates encrypted zero in the same conditions as the Eq. 9. Table 3 shows the values of c
i
computed based on the efficient privacy-preserving comparison protocol (EPPCP) and the IDCP, which are denoted as \({c_{i}^{E}}\) and \({c_{i}^{I}}\), respectively. Table 3 analyzes the existence of zero in \({c_{i}^{E}}\) generated based on the s, \(\acute {d}\), \(\hat {r}\), and \(S_{i+1}=\sum _{j=i+1}^{\ell -1} {\left (\acute {d}_{j}\cdot 2^{j} \:\:- \:\:\hat {r}_{j}\cdot 2^{j}\right)}\) values. Based on this table, the value of \(c_{i}^{IDCP}\) can be zero in two conditions, where \(\{ \acute {d}<\hat {r}, \: s=1,\: \acute {d}_{i}=0, \text {and } \hat {r}_{i}=1\}\) and \(\{ \acute {d}>\hat {r}, \: s=-1,\: \acute {d}_{i}=1, \text {and } \hat {r}_{i}=0\}\). However, \({c_{i}^{E}}\) generates zero in more conditions than \({c_{i}^{I}}\) does. For instance, if \(\{S_{i+1}=2, s=-1, \acute {d}>\hat {r}, \text {and } \acute {d}_{i}=\hat {r}_{i}=1\}\), then \({c_{i}^{E}}=0\). Table 3 shows that values of \({c_{i}^{I}}\) can be zero in the conditions 4 and 5; however, \({c_{i}^{E}}\) values are zero in the conditions 3, 4, 5, and 6 based on the assumed values of S
i+1 for each condition. We note that if \(\acute {d}_{1}\acute {d}_{0}*\hat {r}_{1}\hat {r}_{0}=2\) and \(\acute {d}_{i} =\hat {r}_{i}\) for 2≤i≤ℓ−1, then the value of \({c_{0}^{E}}\) becomes zero. To fix this problem, we compare \(2\acute {d}\) and \(2\hat {r}\) instead of \(\acute {d}\) and \(\hat {r}\). Therefore, Eq. 12 does not generate zero in the conditions 3 and 6. Furthermore, for the comparison protocol to work when \(\acute {d}=\hat {r}\), we compare \(3\acute {d}\) and \(3\hat {r}+1\) instead of \(\acute {d}\) and \(\hat {r}\) respectively, as suggested similarly in [17].
by Eq. 12. In order to do that, we check if Eq. 12 generates encrypted zero in the same conditions as the Eq. 9. Table 3 shows the values of c
i
computed based on the efficient privacy-preserving comparison protocol (EPPCP) and the IDCP, which are denoted as \({c_{i}^{E}}\) and \({c_{i}^{I}}\), respectively. Table 3 analyzes the existence of zero in \({c_{i}^{E}}\) generated based on the s, \(\acute {d}\), \(\hat {r}\), and \(S_{i+1}=\sum _{j=i+1}^{\ell -1} {\left (\acute {d}_{j}\cdot 2^{j} \:\:- \:\:\hat {r}_{j}\cdot 2^{j}\right)}\) values. Based on this table, the value of \(c_{i}^{IDCP}\) can be zero in two conditions, where \(\{ \acute {d}<\hat {r}, \: s=1,\: \acute {d}_{i}=0, \text {and } \hat {r}_{i}=1\}\) and \(\{ \acute {d}>\hat {r}, \: s=-1,\: \acute {d}_{i}=1, \text {and } \hat {r}_{i}=0\}\). However, \({c_{i}^{E}}\) generates zero in more conditions than \({c_{i}^{I}}\) does. For instance, if \(\{S_{i+1}=2, s=-1, \acute {d}>\hat {r}, \text {and } \acute {d}_{i}=\hat {r}_{i}=1\}\), then \({c_{i}^{E}}=0\). Table 3 shows that values of \({c_{i}^{I}}\) can be zero in the conditions 4 and 5; however, \({c_{i}^{E}}\) values are zero in the conditions 3, 4, 5, and 6 based on the assumed values of S
i+1 for each condition. We note that if \(\acute {d}_{1}\acute {d}_{0}*\hat {r}_{1}\hat {r}_{0}=2\) and \(\acute {d}_{i} =\hat {r}_{i}\) for 2≤i≤ℓ−1, then the value of \({c_{0}^{E}}\) becomes zero. To fix this problem, we compare \(2\acute {d}\) and \(2\hat {r}\) instead of \(\acute {d}\) and \(\hat {r}\). Therefore, Eq. 12 does not generate zero in the conditions 3 and 6. Furthermore, for the comparison protocol to work when \(\acute {d}=\hat {r}\), we compare \(3\acute {d}\) and \(3\hat {r}+1\) instead of \(\acute {d}\) and \(\hat {r}\) respectively, as suggested similarly in [17].
4.2 Data packing
According to Table 2, Paillier decryption of [ d] (Eq. 6) dominates more than 62 % of the comparison protocol execution time at Bob side. We decrease the run-time of Paillier decryption by employing data packing similar to [19, 20]. The main idea behind data packing is to efficiently use the message space of the Paillier cryptosystem that is much larger than the values to be compared.
Assume that z and r are ℓ and ℓ+κ-bit integers, respectively. Then, [ d]=[ z+r] is a (ℓ+κ+1)-bit integer. Let the message space of the Paillier cryptosystem be η=p q, then Alice packs ρ=⌊(ℓ+κ+1)/η⌋ into one Paillier message as follows:
and sends \([\!\hat {d}]\) to Bob. Then, Bob computes \(\mathcal {D}_{sk}\left ([\!\hat {d}]\right)\), unpacks ρ different values and performs modulo reduction on each unpacked value. Employing the data packing technique not only reduces the number of very expensive Paillier decryption to be performed but also decreases the number of encrypted messages to be transmitted.
5 Performance analysis
In this section, we analyze the number of operations over ciphertexts, since they are computationally expensive compared to operations on the plaintext and dominate the protocol execution run-time and provide experimental results for run-time performance. For this purpose, we implemented the EPPCP using C++ and SeComLib [26] library, on a Linux machine running Ubuntu 14.04 LTS, with 64-bit microprocessor and 8 GB of RAM. The experiments are repeated for 10,000 comparisons. Table 4 provides more information about parameters and their corresponding values in our implementation.
Table 5 shows the computational complexity of the original DGK comparison protocol, the IDCP, and the EPPCP. Note that the number of multiplications and exponentiations are regarding the computation of  . According to the Table 5, the original DGK comparison protocol suffers from its high computational complexity regarding the number of multiplications and exponentiations over ciphertexts. Veugen [18] presented two improvements to decrease the computational cost of the DGK comparison protocol, namely an efficient method to compute XOR and an algorithm to mask less
. According to the Table 5, the original DGK comparison protocol suffers from its high computational complexity regarding the number of multiplications and exponentiations over ciphertexts. Veugen [18] presented two improvements to decrease the computational cost of the DGK comparison protocol, namely an efficient method to compute XOR and an algorithm to mask less  , which results in a lower number of exponentiations with positive exponent. However, according to Table 5, the new technique of computing XOR have a slight impact on the overall number of multiplications and exponentiations. Moreover, Table 2 shows that computation of
, which results in a lower number of exponentiations with positive exponent. However, according to Table 5, the new technique of computing XOR have a slight impact on the overall number of multiplications and exponentiations. Moreover, Table 2 shows that computation of  takes 15 % of the protocol run-time in Alice (the improvement for computing
takes 15 % of the protocol run-time in Alice (the improvement for computing  [18] is not applied in the implementation); therefore, even a significant improvement over computation of
[18] is not applied in the implementation); therefore, even a significant improvement over computation of  does not provide a significant influence on the overall run-time.
does not provide a significant influence on the overall run-time.
Table 5 shows that the computational complexity of computing  in the EPPCP is decreased to ℓ multiplications over ciphertexts, and there is no exponentiation with positive or negative exponent. According to Table 6, this low computational complexity results in 91 % decrease in computation of
in the EPPCP is decreased to ℓ multiplications over ciphertexts, and there is no exponentiation with positive or negative exponent. According to Table 6, this low computational complexity results in 91 % decrease in computation of  compared to the IDCP. This improvement also reduces the run-time of all computations performed by Alice by 64 %.
compared to the IDCP. This improvement also reduces the run-time of all computations performed by Alice by 64 %.
Table 2 also shows that Paillier decryption dominates 62 % of the IDCP run-time by Bob. According to the Table 6, by deploying data packing the run-time of the Paillier decryption and all Bob’s computations are decreased by 85 and 53 %, respectively.
Table 7 shows the running times of the Paillier decryption (PD), computation of c i , and the total run-time (online phase) of both the EPPCP and the IDCP for different key sizes. It shows that the EPPCP achieves better efficiency compared to the IDCP for the large key sizes.
According to Table 8, running EPPCP 10,000 times takes 41 s, where it takes 93 s for the IDCP. Table 8 also shows that pre-computation phase takes more time in EPPCP as a result of the new method of computing  , which allows performing more initial computations before run-time. The communication cost between Alice and Bob is decreased by 25 % in EPPCP because of using data packing technique.
, which allows performing more initial computations before run-time. The communication cost between Alice and Bob is decreased by 25 % in EPPCP because of using data packing technique.
6 Security and privacy of comparison protocol
In this section, we provide a security sketch of the proposed privacy-preserving comparison protocol in the semi-honest model. For a more elaborate security proof, we refer readers to [25].
As mentioned before, smart meters encrypt the power consumption using the Paillier cryptosystem, which is semantically secure under the decisional composite residuosity assumption (for more information about the security of Paillier cryptosystem, we refer reader to [24]); thus, Alice (data aggregator) has only encrypted values. Here, we show that not only does Bob (utility provider) not learn anything about the given encrypted values but also Alice does not learn any information about encrypted output of the algorithm at the end of the proposed comparison protocol.
Alice computes together with Bob [ zmod2ℓ] without revealing any information about [ z] to him. Since this value reveals information on the distance between a and b; therefore, Alice masks [ z] by adding a random value, [ d]=[z+r], and sends [ d] to Bob instead of [ z]. Since r is a uniformly random (k+ℓ)-bit value, [ z] is statistically indistinguishable from [ d] to Bob.
Bob sends back [ dmod2ℓ] to Alice in the encrypted form, which means she cannot learn any information about the content of [ z], but only [zmod2ℓ]. Then Alice sends  values, which are the masked and the permuted
values, which are the masked and the permuted  values, to Bob who checks the existence of an encrypted zero among given
values, to Bob who checks the existence of an encrypted zero among given  . Therefore, Bob only receives a list of uniformly random values. Moreover, using a binary random value s through computation of
. Therefore, Bob only receives a list of uniformly random values. Moreover, using a binary random value s through computation of  prevents Bob from drawing any conclusions about the result of the comparison by checking
prevents Bob from drawing any conclusions about the result of the comparison by checking  . Since Alice is not authorized to know the result of the comparison, Bob only sends the encrypted value of \(\tilde {\lambda }\), \([\!\tilde {\lambda }]\), to Alice. Then, she can only correct the \([\!\tilde {\lambda }]\) based on s to obtain [ λ] and compute [ z
ℓ
].
. Since Alice is not authorized to know the result of the comparison, Bob only sends the encrypted value of \(\tilde {\lambda }\), \([\!\tilde {\lambda }]\), to Alice. Then, she can only correct the \([\!\tilde {\lambda }]\) based on s to obtain [ λ] and compute [ z
ℓ
].
7 Conclusions
Comparing consumers’ power consumption profiles is a necessary part of smart grids for a number of services including generating personalized recommendations. Since personal profiles contain private information about consumers’ power consumption, privacy-preserving approaches should be considered. One of the most effective approaches is based on using cryptographic tools that enable processing encrypted data. Unfortunately, secure and privacy-sensitive versions of such services are computationally expensive, which hinders the deployment of such protocols in practice. In this paper, we investigated a vital operation that is invoked numerous times during many algorithms, namely comparison, and improve its performance significantly by introducing algorithmic changes and deploying data packing. By doing so, we improve the efficiency of the state-of-the-art secure comparison protocol based on homomorphic encryption. More precisely, we reduce the run-time of computations by the data aggregator and the utility provider by 64 and 52 %, respectively. In terms of overall performance, the proposed comparison protocol is faster than state-of-the-art by 56 % and the communication cost is reduced by 25 %. This improvement in performance leads to a more practical comparison protocol that can be used for designing privacy-preserving protocols.
References
GP Verbong, S Beemsterboer, F Sengers, Smart grids or smart users? Involving users in developing a low carbon electricity economy. Energy Policy. 52:, 117–125 (2013).
I Lampropoulos, G Vanalme, W Kling, in Proceedings of Innovative Smart Grid Technologies Conference Europe (ISGT Europe). A methodology for modeling the behavior of electricity prosumers within the smart grid (IEEE PESGothenburg, 2010), pp. 1–8.
T Jackson, Motivating Sustainable Consumption: A Review of Evidence on Consumer Behaviour and Behavioural Change: a Report to the Sustainable Development Research Network (Centre for Environmental Strategy, University of Surrey, 2005).
S Van Dam, Smart energy management for households. A+BE | Architecture and the Built Environment. 3(5), 1–334 (2013). doi:10.7480/abe.2013.5.
A Spagnolli, N Corradi, L Gamberini, E Hoggan, G Jacucci, C Katzeff, L Broms, L Jönsson, Eco-Feedback on the go: motivating energy awareness. IEEE Comput.44(5), 38–45 (2011).
PC Honebein, RF Cammarano, C Boice, Building a social roadmap for the smart grid. Electr. J.24(4), 78–85 (2011).
V Giordano, F Gangale, G Fulli, MS Jiménez, I Onyeji, A Colta, I Papaioannou, A Mengolini, C Alecu, T Ojala, et al., Smart Grid Projects in Europe: Lessons Learned and Current Developments (Publications Office of the European Union, Luxembourg, 2011).
J Liu, Y Xiao, S Li, W Liang, C Chen, Cyber security and privacy issues in smart grids. IEEE Commun. Surv. Tutor.14(4), 981–997 (2012).
P McDaniel, S McLaughlin, Security and privacy challenges in the smart grid. IEEE Sec Privacy. 7:, 75–77 (2009).
FG Marmol, C Sorge, O Ugus, GM Pérez, Do not snoop my habits: preserving privacy in the smart grid. IEEE Commun. Mag.50(5), 166–172 (2012).
K Birman, M Jelasity, R Kleinberg, E Tremel, Building a secure and privacy-preserving smart grid. ACM SIGOPS Oper. Syst. Rev.49(1), 131–136 (2015).
Z Erkin, G Tsudik, in Applied Cryptography and Network Security (ACNS 2012), Vol. 7341 of Lecture Notes in Computer Science. Private computation of spatial and temporal power consumption with smart meters (Springer, 2012), pp. 561–577.
K Kursawe, G Danezis, M Kohlweiss, in Proceedings of the 11th international conference on Privacy enhancing technologies, PETS’11. Privacy-friendly aggregation for the smart-grid (Springer-VerlagBerlin, Heidelberg, 2011), pp. 175–191. http://dl.acm.org/citation.cfm?id=2032162.2032172.
C Efthymiou, G Kalogridis, in First IEEE International Conference on Smart Grid Communications. Smart grid privacy via anonymization of smart metering data (IEEE, 2010), pp. 238–243.
I Damgard, M Geisler, M Kroigard, A correction to ‘efficient and secure comparison for on-line auctions’. Int. J. Appl. Cryptogr.1(4), 323–324 (2009).
T Veugen, F Blom, S de Hoogh, Z Erkin, Secure comparison protocols in the semi-honest model. IEEE J. Sel. Top. Signal Process.9(7), 1217–1228 (2015).
Z Erkin, M Franz, J Guajardo, S Katzenbeisser, I Lagendijk, T Toft, in Privacy Enhancing Technologies (PET’09), Vol. 5672 of LNCS. Privacy-preserving face recognition (Springer, 2009), pp. 235–253.
T Veugen, in IEEE Workshop on Information Forensics and Security. Improving the DGK comparison protocol (IEEE WIFSTenerife, 2012), pp. 49–54.
JR Troncoso-Pastoriza, S Katzenbeisser, MU Celik, AN Lemma, in ACM Workshop on Multimedia and Security. A secure multidimensional point inclusion protocol (ACM, 2007), pp. 109–120.
T Bianchi, A Piva, M Barni, Composite signal representation for fast and storage-efficient processing of encrypted signals. IEEE Trans. Inf. Forensics Sec.5(1), 180–187 (2010).
M Barni, T Bianchi, D Catalano, Raimondo Di M, R Donida Labati, et al., in ACM Proceedings of the 12th ACM workshop on Multimedia and security. Privacy-Preserving Fingercode Authentication, (2010), pp. 231–240.
MRT Beye, Z Erkin, RL Lagendijk, in Proc. in IEEE Workshop on Information Forensics and Security (WIFS’11). Efficient privacy preserving k-means clustering in a three-party setting, (2011), pp. 1–6.
Z Erkin, T Veugen, T Toft, RL Lagendijk, Generating private recommendations efficiently using homomorphic encryption and data packing. IEEE Trans. Inf. Forensics Sec.7(3), 1053–1066 (2012).
P Paillier, in Eurocrypt ’99. Public-Key Cryptosystems Based on Composite Degree Residuosity Classes (Springer, 1999), pp. 223–238.
I Damgård, M Geisler, M Krøigaard, in Australasian Conference on Information Security and Privacy (ACISP’07), Vol. 4586 of LNCS. Efficient and secure comparison for on-line auctions (Springer, 2007), pp. 416–430.
Cyber Security Group, SeComLib Secure Computation Library. http://cybersecurity.tudelft.nl. Accessed 2013.
Acknowledgements
This publication was supported by Dutch national program COMMIT.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
MN proposed the improvements for the DGK comparison protocol and implemented the EPPCP. ZE and RLL participated in improving the EPPCP in terms of security, carried out performance and security analysis, and contributed in designing, drafting, and revising the manuscript. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Nateghizad, M., Erkin, Z. & Lagendijk, R.L. An efficient privacy-preserving comparison protocol in smart metering systems. EURASIP J. on Info. Security 2016, 11 (2016). https://doi.org/10.1186/s13635-016-0033-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13635-016-0033-4
 , to Alice.
, to Alice. as follows,
as follows,
 , and i=0,…,ℓ−1.
, and i=0,…,ℓ−1. with a uniformly random
with a uniformly random 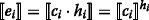
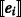 and sends them to Bob. Note that if c
t
=0, where t
and sends them to Bob. Note that if c
t
=0, where t values. If none of the
values. If none of the  values are encrypted zero then he sets
values are encrypted zero then he sets  . Veugen [
. Veugen [ when
when 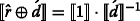 (recall that Alice and Bob have access to values
(recall that Alice and Bob have access to values  to obtain a more efficient protocol.
to obtain a more efficient protocol.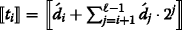 , and sends
, and sends 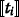 to Alice.
to Alice. .
. as follows,
as follows,