- Research Article
- Open access
- Published:
Binary Biometric Representation through Pairwise Adaptive Phase Quantization
EURASIP Journal on Information Security volume 2011, Article number: 543106 (2011)
Abstract
Extracting binary strings from real-valued biometric templates is a fundamental step in template compression and protection systems, such as fuzzy commitment, fuzzy extractor, secure sketch, and helper data systems. Quantization and coding is the straightforward way to extract binary representations from arbitrary real-valued biometric modalities. In this paper, we propose a pairwise adaptive phase quantization (APQ) method, together with a long-short (LS) pairing strategy, which aims to maximize the overall detection rate. Experimental results on the FVC2000 fingerprint and the FRGC face database show reasonably good verification performances.
1. Introduction
Extracting binary biometric strings is a fundamental step in template compression and protection [1]. It is well known that biometric information is unique, yet inevitably noisy, leading to intraclass variations. Therefore, the binary strings are desired not only to be discriminative, but also have to low intraclass variations. Such requirements translate to both low false acceptance rate (FAR) and low false rejection rate (FRR). Additionally, from the template protection perspective, we know that general biometric information is always public, thus any person has some knowledge of the distribution of biometric features. Furthermore, the biometric bits in the binary string should be independent and identically distributed (i.i.d.), in order to maximize the attacker's efforts in guessing the target template.
Several biometric template protection concepts have been published. Cancelable biometrics [2, 3] distort the image of a face or a fingerprint by using a one-way geometric distortion function. The fuzzy vault method [4, 5] is a cryptographic construction allowing to store a secret in a vault that can be locked using a possibly unordered set of features, for example, fingerprint minutiae. A third group of techniques, containing fuzzy commitment [6], fuzzy extractor [7], secure sketch [8], and helper data system [9–13], derive a binary string from a biometric measurement and store an irreversibly hashed version of the string with or without binding a crypto key. In this paper, we adopt the third group of techniques.
The straightforward way to extract binary strings is quantization and coding of the real-valued features. So far, many works [9–11, 14–20] have adopted the bit extraction framework shown in Figure 1, involving two tasks: (1) designing a one-dimensional quantizer and (2) determining the number of quantization bits for every feature. The final binary string is then the concatenation of the output bits from all the individual features.
Designing a one-dimensional quantizer relies on two probability density functions (PDFs): the background PDF and the genuine user PDF, representing the probability density of the entire population and the genuine user, respectively. Based on the two PDFs, quantization intervals are determined to maximize the detection rate, subject to a given FAR, according to the Neyman-Pearson criterion. So far, a number of one-dimensional quantizers have been proposed [9–11, 14–17], as categorized in Table 1. Quantizers in [9–11] are userindependent, constructed merely from the background PDF, whereas quantizers in [14–17] are user-specific, constructed from both the genuine user PDF and the background PDF. Theoretically, user-specific quantizers provide better verification performances. Particularly, the likelihood ratio-based quantizer [17], among all the quantizers, is optimal in the Neyman-Pearson sense. Quantizers in [9, 14–16] have equal-width intervals. Unfortunately, this leads to potential threats: features obtain higher probabilities in certain quantization intervals than in others, and thus attackers can easily find the genuine interval by continuously guessing the one with the highest probability. To avoid this problem, quantizers in [10, 11, 17] have equal-probability intervals, ensuring i.i.d. bits.
Apart from the one-dimensional quantizer design, some papers focus on assigning a varying number of quantization bits to each feature. So far, several bit allocation principles have been proposed: fixed bit allocation (FBA) [10, 11, 17] simply assigns a fixed number of bits to each feature. On the contrary, the detection rate optimized bit allocation (DROBA) [19] and the area under the FRR curve optimized bit allocation (AUF-OBA) [20], assign a variable number of bits to each feature, according to the features' distinctiveness. Generally, AUF-OBA and DROBA outperform FBA.
In this paper, we deal with quantizer design rather than assigning the quantization bits to features. Although one-dimensional quantizers yield reasonably good performances, a problem remains: independency between all feature dimensions is usually difficult to achieve. Furthermore, one-dimensional quantization leads to inflexible quantization intervals, for instance, the orthogonal boundaries in the two-dimensional feature space, as illustrated in Figure 2(a). Contrarily, two-dimensional quantizers, with an extra degree of freedom, bring more flexible quantizer structures. Therefore, a user-independent pairwise polar quantization was proposed in [21]. The polar quantizer is illustrated in Figure 2(b), where both the magnitude and the phase intervals are determined merely by the background PDF. In principle, polar quantization is less prone to outliers and less strict on independency of the features, when the genuine user PDF is located far from the origin. Therefore, in [21], two pairing strategies, the long-long and the long-short pairing, were proposed for the magnitude and the phase, respectively. Both pairing strategies use the Euclidean distances between each feature's mean and the origin. Results showed that the magnitude yields a poor verification performance, whereas the phase yields a good performance. The two-dimensional quantization-based bit extraction framework, including an extra feature pairing step, is illustrated in Figure 3.
The two-dimensional illustration of (a) the one-dimensional quantizer boundaries (dash line) and (b) the userindependent polar quantization boundaries (dash line). The genuine user PDF is in red and the background PDF is in blue. The detection rate and the FAR are the integral of both PDFs in the pink area.
The bits extraction framework based on two-dimensional quantization and coding, where D denotes the number of features; K denotes the number of feature pairs; c k denotes the feature index for the kth feature pair (k=1,…,K); s k denotes the corresponding quantized bits. The final output binary string is S=s 1 s 2 s K .
Since the phase quantization has shown in [21] to yield a good performance, in this paper, we propose a user-specific adaptive phase quantizer (APQ). Furthermore, we introduce a Mahalanobis distance-based long-short (LS) pairing strategy that by good approximation maximizes the theoretical overall detection rate at zero Hamming distance threshold.
In Section 2 we introduce the adaptive phase quantizer (APQ), with simulations in a particular case with independent Gaussian densities. In Section 3 the long-short (LS) pairing strategy is introduced to compose pairwise features. In Section 4, we give some experimental results on the FVC2000 fingerprint database and the FRGC face database. In Section 5 the results are discussed and conclusions are drawn in Section 6.
2. Adaptive Phase Quantizer (APQ)
In this section, we first introduce the APQ. Afterwards, we discuss its performance in a particular case where the feature pairs have independent Gaussian densities.
2.1. Adaptive Phase Quantizer (APQ)
The adaptive phase quantization can be applied to a two-dimensional feature vector if its background PDF is circularly symmetric about the origin. Let  denote a two-dimensional feature vector. The phase
denote a two-dimensional feature vector. The phase  , ranging from
, ranging from  , is defined as its counterclockwise angle from the
, is defined as its counterclockwise angle from the  -axis. For a genuine user
-axis. For a genuine user  , a
, a  -bit APQ is then constructed as
-bit APQ is then constructed as


where  represents the
represents the  th quantization interval, determined by the quantization step
th quantization interval, determined by the quantization step  and an offset angle
and an offset angle  . Every quantization interval is uniquely encoded using
. Every quantization interval is uniquely encoded using  bits. Let
bits. Let  be the mean of the genuine feature vector
be the mean of the genuine feature vector  , then among the intervals, the genuine interval
, then among the intervals, the genuine interval  , which is assigned for the genuine user
, which is assigned for the genuine user  , is referred to as
, is referred to as

that is,  is the interval where the mean
is the interval where the mean  is located. In Figure 4 we give an illustration of a
is located. In Figure 4 we give an illustration of a  -bit APQ.
-bit APQ.
The adaptive offset  in (2) is determined by the background PDF
in (2) is determined by the background PDF  as well as the genuine user PDF
as well as the genuine user PDF  : given both PDFs and an arbitrary offset
: given both PDFs and an arbitrary offset  , the theoretical detection rate
, the theoretical detection rate  and the FAR
and the FAR  at zero Hamming distance threshold are
at zero Hamming distance threshold are


Given that the background PDF is circularly symmetric, (5) is independent of  . Thus, (5) becomes
. Thus, (5) becomes

Therefore, the optimal  is determined by maximizing the detection rate in (4):
is determined by maximizing the detection rate in (4):

After the  is determined, the quantization intervals are constructed from (2). Additionally, the detection rate of the APQ is
is determined, the quantization intervals are constructed from (2). Additionally, the detection rate of the APQ is

Essentially, APQ has both equal-width and equal-probability intervals, with rotation offset  that maximizes the detection rate.
that maximizes the detection rate.
2.2. Simulations on Independent Gaussian Densities
We investigate the APQ performances on synthetic data, in a particular case where the feature pairs have independent Gaussian densities. That is, the background PDF of both features are normalized as zero mean and unit variance, that is,  . Similarly, the genuine user PDFs are
. Similarly, the genuine user PDFs are  and
and  . Since the two features are independent, the two-dimensional joint background PDF
. Since the two features are independent, the two-dimensional joint background PDF  and the joint genuine user PDF
and the joint genuine user PDF  are
are

According to (6), the FAR for a  -bit APQ is fixed to
-bit APQ is fixed to  . Therefore, we only have to investigate the detection rate in (8) regarding the genuine user PDF
. Therefore, we only have to investigate the detection rate in (8) regarding the genuine user PDF  , defined by the
, defined by the  and
and  values. In Figure 5, we show the detection rate
values. In Figure 5, we show the detection rate  of the
of the  -bit APQ (
-bit APQ ( , 2, 3, 4), when
, 2, 3, 4), when  is modeled as
is modeled as  ;
;  ;
;  ,
,  , at various
, at various  ,
,  locations for optimal
locations for optimal  . The white pixels represent high values of the detection rate whilst the black pixels represent low values. The
. The white pixels represent high values of the detection rate whilst the black pixels represent low values. The  appears to depend more on how far the features are from the origin than on the direction of the features. This is due to the rotation adaptive property. In general, the
appears to depend more on how far the features are from the origin than on the direction of the features. This is due to the rotation adaptive property. In general, the  is higher when the genuine user PDF has smaller
is higher when the genuine user PDF has smaller  and larger
and larger  for both features. Either decreasing the
for both features. Either decreasing the  or increasing the
or increasing the  deteriorates the performance.
deteriorates the performance.
To generalize such property, we define a Mahalanobis distance  for feature
for feature  as
as

Given the Mahalanobis distances  ,
,  of two features, we define
of two features, we define  for this feature pair as
for this feature pair as

In Figure 6 we give some simulation results for the relation between  and
and  . The parameters
. The parameters  and
and  for the genuine user PDF
for the genuine user PDF  are modeled as four
are modeled as four  combinations at various
combinations at various  locations. For every
locations. For every  -
- setting, we plot its
setting, we plot its  and
and  . We observe that the detection rate
. We observe that the detection rate  tends to increase when the feature pair Mahalanobis distance
tends to increase when the feature pair Mahalanobis distance  increases, although not always monotonically.
increases, although not always monotonically.
We further compare the detection rate of APQ to that of the one-dimensional fixed quantizer (FQ) [17]. In order to compare with the 2-bit APQ at the same FAR, we choose a 1-bit FQ ( ) for every feature dimension. In Figure 7 we show the ratio of their detection rates (
) for every feature dimension. In Figure 7 we show the ratio of their detection rates ( ) at various
) at various  -
- values. The white pixels represent high values whilst the black pixels represent low values. It is observed that APQ consistently outperforms FQ, especially when the mean of the genuine user PDF is located far away from the origin and close to the FQ boundary, namely, the
values. The white pixels represent high values whilst the black pixels represent low values. It is observed that APQ consistently outperforms FQ, especially when the mean of the genuine user PDF is located far away from the origin and close to the FQ boundary, namely, the  -axis and
-axis and  -axis. In fact, the two 1-bit FQ works as a special case of the 2-bit APQ, with
-axis. In fact, the two 1-bit FQ works as a special case of the 2-bit APQ, with  .
.
3. Biometric Binary String Extraction
The APQ can be directly applied to two-dimensional features, such as Iris [22], while for arbitrary features, we have the freedom to pair the features. In this section, we first formulate the pairing problem, which in practice is difficult to solve. Therefore, we simplify this problem and then propose a long-short pairing strategy (LS) with low computational complexity.
3.1. Problem Formulation
The aim for extracting biometric binary string is for a genuine user  who has
who has  features, we need to determine a strategy to pair these
features, we need to determine a strategy to pair these  features into
features into  pairs, in such way that the entire
pairs, in such way that the entire  -bit binary string (
-bit binary string ( ) obtains optimal classification performance, when every feature pair is quantized by a
) obtains optimal classification performance, when every feature pair is quantized by a  -bit APQ. Assuming that the
-bit APQ. Assuming that the  feature pairs are statistically independent, we know from [19] that when applying a Hamming distance classifier, zero Hamming distance threshold gives a lower bound for both the detection rate and the FAR. Therefore, we decide to optimize this lower bound classification performance.
feature pairs are statistically independent, we know from [19] that when applying a Hamming distance classifier, zero Hamming distance threshold gives a lower bound for both the detection rate and the FAR. Therefore, we decide to optimize this lower bound classification performance.
Let  , (
, ( ) be the
) be the  th pair of feature indices, and
th pair of feature indices, and  a valid pairing configuration containing
a valid pairing configuration containing  feature index pairs such that every feature index only appears once. For instance,
feature index pairs such that every feature index only appears once. For instance,  is not valid because it contains the same feature and therefore cannot be included in
is not valid because it contains the same feature and therefore cannot be included in  . Also,
. Also,  is not a valid pairing configuration because the index value "1" appears twice. The overall FAR (
is not a valid pairing configuration because the index value "1" appears twice. The overall FAR ( ) and the overall detection rate (
) and the overall detection rate ( ), at zero Hamming distance threshold are
), at zero Hamming distance threshold are


where  and
and  are the FAR and the detection rate for the
are the FAR and the detection rate for the  th feature pair, computed from (6) and (8). Furthermore, according to (6),
th feature pair, computed from (6) and (8). Furthermore, according to (6),  becomes
becomes

which is independent of  . Therefore, we only need to search for a user-specific pairing configuration
. Therefore, we only need to search for a user-specific pairing configuration  , that maximizes the overall detection rate in (13). Solving the optimization problem is formulated as
, that maximizes the overall detection rate in (13). Solving the optimization problem is formulated as

The detection rate  given a feature pair
given a feature pair  is computed from (8). Considering that the performance at zero Hamming distance threshold indeed pinpoints the minimum FAR and detection rate value on the receiver operating characteristic curve (ROC), optimizing such point in (15) essentially provides a maximum lower bound for the ROC curve.
is computed from (8). Considering that the performance at zero Hamming distance threshold indeed pinpoints the minimum FAR and detection rate value on the receiver operating characteristic curve (ROC), optimizing such point in (15) essentially provides a maximum lower bound for the ROC curve.
3.2. Long-Short Pairing
There are two problems in solving (15): first, it is often not possible to compute  in (8), due to the difficulties in estimating the genuine user PDF
in (8), due to the difficulties in estimating the genuine user PDF  . Additionally, even if the
. Additionally, even if the  can be accurately estimated, a brute-force search would involve
can be accurately estimated, a brute-force search would involve  evaluations of the overall detection rate, which renders a brute-force search unfeasible for realistic values of
evaluations of the overall detection rate, which renders a brute-force search unfeasible for realistic values of  . Therefore, we propose to simplify the problem definition in (15) as well as the optimization searching approach.
. Therefore, we propose to simplify the problem definition in (15) as well as the optimization searching approach.
Simplified Problem Definition
In Section 2.2 we observed a useful relation between  and
and  for the APQ: A feature pair with a higher
for the APQ: A feature pair with a higher  would approximately also obtain a higher detection rate
would approximately also obtain a higher detection rate  for APQ. Therefore, we simplify (15) into
for APQ. Therefore, we simplify (15) into

with  defined in (11). Furthermore, instead of brute force searching, we propose a simplified optimization searching approach: the long-short (LS) pairing strategy.
defined in (11). Furthermore, instead of brute force searching, we propose a simplified optimization searching approach: the long-short (LS) pairing strategy.
Long-Short (LS) Pairing
For the genuine user  , sort the set
, sort the set  from largest to smallest into a sequence of ordered feature indices
from largest to smallest into a sequence of ordered feature indices  . The index for the
. The index for the  th feature pair is then
th feature pair is then

The computational complexity of the LS pairing is only  . Additionally, it is applicable to arbitrary feature types and independent of the number of quantization bits
. Additionally, it is applicable to arbitrary feature types and independent of the number of quantization bits  . Note that this LS pairing is similar to the pairing strategy proposed in [21], where Euclidean distances are used. In fact, there are other alternative pairing strategies, for instance greedy or long-long pairing [21]. However, in terms of the entire binary string performance, these methods are not as good as the approach presented in this paper, especially when
. Note that this LS pairing is similar to the pairing strategy proposed in [21], where Euclidean distances are used. In fact, there are other alternative pairing strategies, for instance greedy or long-long pairing [21]. However, in terms of the entire binary string performance, these methods are not as good as the approach presented in this paper, especially when  is large. Therefore, in this paper, we choose the long-short pairing strategy, providing a compromise between the classification performance and computational complexity.
is large. Therefore, in this paper, we choose the long-short pairing strategy, providing a compromise between the classification performance and computational complexity.
4. Experiments
In this section we test the pairwise phase quantization (LS + APQ) on real data. First we present a simplified APQ, which is employed in all the experiments. Afterwards, we verify the relation between  and
and  for real data. We also show some examples of LS pairing results. Then we investigate the verification performances while varying the input feature dimensions (
for real data. We also show some examples of LS pairing results. Then we investigate the verification performances while varying the input feature dimensions ( ) and the number of quantization bits per feature pair (
) and the number of quantization bits per feature pair ( ). The results are further compared to the one-dimensional fixed quantization (1D FQ) [17] as well as the the FQ in combined with the DROBA bit allocation principle (FQ + DROBA).
). The results are further compared to the one-dimensional fixed quantization (1D FQ) [17] as well as the the FQ in combined with the DROBA bit allocation principle (FQ + DROBA).
4.1. Experimental Setup
We tested the pairwise phase quantization on two real data sets: the FVC2000(DB2) fingerprint database [23] and the FRGC(version 1) face database [24].
(i)FVC2000: The FVC2000(DB2) fingerprint data set contains 8 images of 110 users. The features were extracted in a fingerprint recognition system that was used in [10]. As illustrated in Figure 8, the raw features contain two types of information: the squared directional field in both  and
and  directions and the Gabor response in 4 orientations (0,
directions and the Gabor response in 4 orientations (0,  ,
,  ,
,  ). Determined by a regular grid of 16 by 16 points with spacing of 8 pixels, measurements are taken at 256 positions, leading to a total of 1536 elements.
). Determined by a regular grid of 16 by 16 points with spacing of 8 pixels, measurements are taken at 256 positions, leading to a total of 1536 elements.
(ii)FRGC: The FRGC(version 1) face data set contains 275 users with a different number of images per user, taken under both controlled and uncontrolled conditions. The number of samples  per user ranges from 4 to 36. The image size was
per user ranges from 4 to 36. The image size was  . From that a region of interest (ROI) with 8762 pixels was taken as illustrated in Figure 9.
. From that a region of interest (ROI) with 8762 pixels was taken as illustrated in Figure 9.
A limitation of biometric compression or protection is that it is not possible to conduct the user-specific image alignment, because the image or other alignment information cannot be stored. Therefore, in this paper, we applied basic absolute alignment methods: the fingerprint images are aligned according to a standard core point position; the face images are aligned according to a set of four standard landmarks, that is, eyes, nose and mouth.
We randomly selected different users for training and testing and repeated our experiments with a number of trials. The data division is described in Table 2, where  is the number of samples per user that varies in the experiments.
is the number of samples per user that varies in the experiments.
Our experiments involved three steps: training, enrollment, and verification. (1) In the training step, we first applied a combined PCA/LDA method [25] on a training set. The obtained transformation was then applied to both the enrollment and verification sets. We assume that the measurements have a Gaussian density, thus after the PCA transformation, the extracted features are assumed to be statistically independent. The goal of applying PCA/LDA in the training step is to extract independent features so that by pairing them we could subsequently obtain independent feature pairs, which meet our problem requirements. Note that for FVC2000, since we have only 80 users in the training set, applying LDA results in very limited number of features (e.g.,  ). Therefore, we relax the independency requirement for the genuine user by applying only the PCA transformation. (2) In the enrollment step, for every genuine user
). Therefore, we relax the independency requirement for the genuine user by applying only the PCA transformation. (2) In the enrollment step, for every genuine user  , the LS pairing was first applied, resulting in the user-specific pairing configuration
, the LS pairing was first applied, resulting in the user-specific pairing configuration  . The pairwise features were further quantized through a
. The pairwise features were further quantized through a  -bit APQ with the adaptive angle
-bit APQ with the adaptive angle  , and assigned with a Gray code [26]. The concatenation of the codes from
, and assigned with a Gray code [26]. The concatenation of the codes from  feature pairs formed the
feature pairs formed the  -bit target binary string
-bit target binary string  . Both
. Both  and the quantization information (
and the quantization information ( ) were stored for each genuine user. (3) In the verification step, the features of the query user were quantized and coded according to the quantization information (
) were stored for each genuine user. (3) In the verification step, the features of the query user were quantized and coded according to the quantization information ( ) of the claimed identity, leading to a query binary string
) of the claimed identity, leading to a query binary string  . Finally, the decision was made by comparing the Hamming distance between the query and the target string.
. Finally, the decision was made by comparing the Hamming distance between the query and the target string.
4.2. Simplified APQ
In practice, computing the optimal offset angle  for APQ in (7) is difficult, because it is hard to find a closed-form solution
for APQ in (7) is difficult, because it is hard to find a closed-form solution  . Besides, it is often impossible to accurately estimate the underlying genuine user PDF
. Besides, it is often impossible to accurately estimate the underlying genuine user PDF  , due to the limited number of available samples per user. Therefore, instead of
, due to the limited number of available samples per user. Therefore, instead of  , we propose an approximate solution
, we propose an approximate solution  . For genuine user
. For genuine user  , let the mean of the two-dimensional feature vector be
, let the mean of the two-dimensional feature vector be  , and its phase be
, and its phase be  , the approximate offset angle
, the approximate offset angle  is then computed as
is then computed as

where  . We give an illustration of computing
. We give an illustration of computing  in Figure 10. The approximate solution
in Figure 10. The approximate solution  in fact maximizes the product of two Euclidean distances, namely, the distance of the mean vector
in fact maximizes the product of two Euclidean distances, namely, the distance of the mean vector  to both the lower and the higher genuine interval boundaries.
to both the lower and the higher genuine interval boundaries.
Note that when the two features have independent Gaussian density with equal standard deviation,  . Thus, in that case, the simplified APQ equals the original APQ. In Figure 11, we illustrates an example of the detection rate ratio between the simplified and the original APQ, where both features are modeled as Gaussian with different standard deviations, for example,
. Thus, in that case, the simplified APQ equals the original APQ. In Figure 11, we illustrates an example of the detection rate ratio between the simplified and the original APQ, where both features are modeled as Gaussian with different standard deviations, for example,  ,
,  . The white pixels represent high values whilst the black pixels represent low values. Results show that the simplified APQ is only slightly worse than the original APQ when the mean of the two-dimensional feature
. The white pixels represent high values whilst the black pixels represent low values. Results show that the simplified APQ is only slightly worse than the original APQ when the mean of the two-dimensional feature  is close to the origin. However, if we apply APQ after the LS pairing, we would expect that the overall selected pairwise features are located farther away from the origin. In such cases, the simplified APQ works almost the same as the original APQ. In Figure 12 we illustrate the differences of the rotation angle between the original APQ and the simplified APQ, computed from (7) and (18), respectively. These differences are computed from 50 feature pairs for both FVC2000 and FRGC. The results show that there is no much differences between the rotation angle. Additionally, the simplified APQ is much simpler, avoiding the problem of estimating the underlying genuine user PDF
is close to the origin. However, if we apply APQ after the LS pairing, we would expect that the overall selected pairwise features are located farther away from the origin. In such cases, the simplified APQ works almost the same as the original APQ. In Figure 12 we illustrate the differences of the rotation angle between the original APQ and the simplified APQ, computed from (7) and (18), respectively. These differences are computed from 50 feature pairs for both FVC2000 and FRGC. The results show that there is no much differences between the rotation angle. Additionally, the simplified APQ is much simpler, avoiding the problem of estimating the underlying genuine user PDF  . For these reasons, we employed this simplified APQ in all the following experiments (Section 4.3 to Section 4.5).
. For these reasons, we employed this simplified APQ in all the following experiments (Section 4.3 to Section 4.5).
4.3. APQ 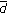 -
-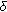 Property
Property
In this section we test the relation between the APQ detection rate  and the pairwise feature's distance
and the pairwise feature's distance  on both data sets. The goal is to see whether the real data exhibit the same
on both data sets. The goal is to see whether the real data exhibit the same  property as we found with synthetic data in Section 2.2: the feature pairs with higher
property as we found with synthetic data in Section 2.2: the feature pairs with higher  obtains higher detection rate
obtains higher detection rate  .
.
During the enrollment, for every genuine user, we conducted a random pairing. For every feature pair, we computed their  value according to (11). Afterwards, we applied the
value according to (11). Afterwards, we applied the  -bit APQ quantizer to every feature pair. In the verification, for every feature pair, we computed the Hamming distance between the
-bit APQ quantizer to every feature pair. In the verification, for every feature pair, we computed the Hamming distance between the  -bits from the genuine user and the
-bits from the genuine user and the  -bits from the imposters; that is, we count as a detection if the
-bits from the imposters; that is, we count as a detection if the  -bit genuine query string obtains zero Hamming distance as compared to the target string. Similarly, we count as a false acceptance if the
-bit genuine query string obtains zero Hamming distance as compared to the target string. Similarly, we count as a false acceptance if the  -bit imposter query string obtains zero Hamming distance as compared to the target string. We then repeated this process over all feature pairs as well as all genuine users, in order to ensure that the results we obtain are neither user or feature biased. Finally, in Figure 13, we plot the relations between the
-bit imposter query string obtains zero Hamming distance as compared to the target string. We then repeated this process over all feature pairs as well as all genuine users, in order to ensure that the results we obtain are neither user or feature biased. Finally, in Figure 13, we plot the relations between the  and the
and the  . The points we plot are averaged according to the bins of
. The points we plot are averaged according to the bins of  , when
, when  . Results show that for the real data, the larger
. Results show that for the real data, the larger  is, consistently the higher detection rate we obtain. Additionally, the FAR performance is indeed independent of pairing and equals the theoretical value
is, consistently the higher detection rate we obtain. Additionally, the FAR performance is indeed independent of pairing and equals the theoretical value  .
.
4.4. LS Pairing Performance
In this section we test the LS pairing performances. We give an example of FVC2000 at  . Figure 14(a) shows the histogram of
. Figure 14(a) shows the histogram of  for all single features over all the genuine users. Around
for all single features over all the genuine users. Around  of them are close to zero, suggesting low quality features. After LS pairing, the histogram of the pairwise
of them are close to zero, suggesting low quality features. After LS pairing, the histogram of the pairwise  values are shown in Figure 14(b), as compared with the random pairing. In Figure 14(c), we illustrate the 25 pairwise features in terms of independent Gaussian densities, for one specific genuine user. Figures 14(b) and 14(c) shows that after LS pairing, a large proportion of feature pairs have relatively moderate "size" densities and moderate
values are shown in Figure 14(b), as compared with the random pairing. In Figure 14(c), we illustrate the 25 pairwise features in terms of independent Gaussian densities, for one specific genuine user. Figures 14(b) and 14(c) shows that after LS pairing, a large proportion of feature pairs have relatively moderate "size" densities and moderate  values. Thus it avoids small
values. Thus it avoids small  values and effectively maximizes (16).
values and effectively maximizes (16).
4.5. Verification Performance
We test the performances of LS + APQ at various numbers of input features  as well as various numbers of quantization bits
as well as various numbers of quantization bits  . The performances are further compared with the one-dimensional fixed quantization (1D FQ) [17]. The EER results for FVC2000 and FRGC are shown in Table 3 and Figure 15.
. The performances are further compared with the one-dimensional fixed quantization (1D FQ) [17]. The EER results for FVC2000 and FRGC are shown in Table 3 and Figure 15.
 and various numbers of quantization bits
and various numbers of quantization bits  , for (a) FVC2000 and (b) FRGC.
, for (a) FVC2000 and (b) FRGC.Both data sets show that by increasing the number of features  at a fixed
at a fixed  -bit quantization per feature pair, the performances of LS + APQ improves and becomes stable. Additionally, given
-bit quantization per feature pair, the performances of LS + APQ improves and becomes stable. Additionally, given  features, the overall performances of LS + APQ are relatively good only when
features, the overall performances of LS + APQ are relatively good only when  . However, when
. However, when  , the performances become poor. For FVC2000, an average of 1-bit per feature pair gives the lowest EER, while for FRGC, the lowest EER allows 2-bit per feature pair. In Figure 16, we give their FAR/FRR performances at the best
, the performances become poor. For FVC2000, an average of 1-bit per feature pair gives the lowest EER, while for FRGC, the lowest EER allows 2-bit per feature pair. In Figure 16, we give their FAR/FRR performances at the best  , with
, with  from 1 to 4, and the FAR/FRR performances at the best
from 1 to 4, and the FAR/FRR performances at the best  are given in Table 5.
are given in Table 5.
 -
- setting.
setting.We further compare the LS + APQ with the 1D FQ. In order to compare at the same string length, we compare the  -bit 1D FQ with the
-bit 1D FQ with the  -bit LS + APQ. The EER performances in Figure 15 show that in general when
-bit LS + APQ. The EER performances in Figure 15 show that in general when  , LS + APQ outperforms 1D FQ. However, when
, LS + APQ outperforms 1D FQ. However, when  , LS + APQ is no longer competitive to 1D FQ. In Figure 17, we give an example of comparing the FAR/FRR performances of LS + APQ and 1D FQ, on FRGC. Since both APQ and FQ provide equal-probability intervals, they yield almost the same FAR performance. On the other hand, LS + APQ obtains lower FRR as compared with 1D FQ.
, LS + APQ is no longer competitive to 1D FQ. In Figure 17, we give an example of comparing the FAR/FRR performances of LS + APQ and 1D FQ, on FRGC. Since both APQ and FQ provide equal-probability intervals, they yield almost the same FAR performance. On the other hand, LS + APQ obtains lower FRR as compared with 1D FQ.
In [19], it was shown that FQ in combination with the DROBA adaptive bit allocation principle (FQ + DROBA) provides considerably good performances. Therefore, we compare the LS + APQ with the FQ + DROBA. In order to compare both methods at the same  -
- setting, for LS + APQ, we extract only
setting, for LS + APQ, we extract only  features from the
features from the  features, thus
features, thus  pairs from the LS pairing. Afterwards, we apply the 2-bit APQ for every feature pair (see Figure 3). In this case,
pairs from the LS pairing. Afterwards, we apply the 2-bit APQ for every feature pair (see Figure 3). In this case,  . Table 6 shows the EER performances of LS + APQ and FQ + DROBA at several different
. Table 6 shows the EER performances of LS + APQ and FQ + DROBA at several different  -
- settings. Results show that LS + APQ obtains slightly better performances than FQ + DROBA.
settings. Results show that LS + APQ obtains slightly better performances than FQ + DROBA.
 -
- settings, for (a) FVC2000 and (b) FRGC.
settings, for (a) FVC2000 and (b) FRGC.5. Discussion
Essentially, the pairwise phase quantization involves two user-specific adaptation steps: the long-short (LS) pairing, as well as the adaptive phase quantization (APQ). From the pairing's perspective, although we only quantize the phase, the magnitude information (i.e. the feature mean) is not discarded. Instead, it is employed in the LS pairing strategy to facilitate extracting distinctive phase bits. Additionally, although with low computational complexity, the LS pairing strategy is effective for arbitrary feature densities. From the quantizer's perspective, quantizing in phase domain has the advantage that a circularly symmetric two-dimensional feature density results in a simple uniform phase density. Additionally, we apply user-specific phase adaptation. As a result, the extracted phase bits are not only distinctive but also robust to over-fitting. However, the experimental results imply that such advantages only exist when  . To summarize, as illustrated in Figure 18, the LS pairing is a user-specific resampling procedure that provides simple unform but distinctive phase densities. The APQ further enhances the feature distinctiveness by adjusting the user-specific phase quantization intervals.
. To summarize, as illustrated in Figure 18, the LS pairing is a user-specific resampling procedure that provides simple unform but distinctive phase densities. The APQ further enhances the feature distinctiveness by adjusting the user-specific phase quantization intervals.
6. Conclusion
Extracting binary biometric strings is a fundamental step in biometric compression and template protection. Unlike many previous work which quantize features individually, in this paper, we propose a pairwise adaptive phase quantization (APQ), together with a long-short (LS) pairing strategy, which aims to maximize the overall detection rate. Experimental results on the FVC2000 and the FRGC database show reasonably good verification performances.
References
Jain AK, Nandakumar K, Nagar A: Biometric template security. EURASIP Journal on Advances in Signal Processing 2008., 2008:
Ratha NK, Connell JH, Bolle RM: Enhancing security and privacy in biometrics-based authentication systems. IBM Systems Journal 2001, 40(3):614-634.
Ratha NK, Chikkerur S, Connell JH, Bolle RM: Generating cancelable fingerprint templates. IEEE Transactions on Pattern Analysis and Machine Intelligence 2007, 29(4):561-572.
Juels A, Sudan M: A fuzzy vault scheme. Designs, Codes, and Cryptography 2006, 38(2):237-257. 10.1007/s10623-005-6343-z
Nandakumar K, Jain AK, Pankanti S: Fingerprint-based fuzzy vault: implementation and performance. IEEE Transactions on Information Forensics and Security 2007, 2(4):744-757.
Juels A, Wattenberg M: Fuzzy commitment scheme. Proceedings of the 6th ACM Conference on Computer and Communications Security (ACM CCS '99), November 1999 28-36.
Dodis Y, Reyzin L, Smith A: Fuzzy extractors: how to generate strong keys from biometrics and other noisy data. Proceedings of International Conference on the Theory and Applications of Cryptographic Techniques, May 2004, Lecture Notes in Computer Science 3027: 523-540.
Chang EC, Roy S: Robust extraction of secret bits from minutiae. Proceedings of the 2nd International Conference on Biometrics (ICB '07), 2007, Lecture Notes in Computer Science 4642: 750-759.
Linnartz J-P, Tuyls P: New shielding functions to enhance privacy and prevent misuse of biometrie templates. Proceedings of Audio-and Video-Based Biometrie Person Authentication (AVBPA '03), 2003, Guildford, UK, Lecture Notes in Computer Science 2688: 393-402.
Tuyls P, Akkermans AHM, Kevenaar TAM, Schrijen G-J, Bazen AM, Veldhuis RNJ: Practical biometric authentication with template protection. Proceedings of the 5th International Conference on Audio-and Video-Based Biometric Person Authentication (AVBPA '05), July 2005, Hilton Rye Town, NY, USA, Lecture Notes in Computer Science 3546: 436-446.
Kevenaar TAM, Schrijen GJ, van der Veen M, Akkermans AHM, Zuo F: Face recognition with renewable and privacy preserving binary templates. Proceedings of the 4th IEEE Workshop on Automatic Identification Advanced Technologies (AUTO ID '05), October 2005, New York, NY, USA 21-26.
Hao F, Anderson R, Daugman J: Combining crypto with biometrics effectively. IEEE Transactions on Computers 2006, 55(9):1081-1088.
Teoh ABJ, Goh A, Ngo DCL: Random multispace quantization as an analytic mechanism for BioHashing of biometric and random identity inputs. IEEE Transactions on Pattern Analysis and Machine Intelligence 2006, 28(12):1882-1901.
Vielhauer C, Steinmetz R, Mayerhöfer A: Biometric hash based on statistical features of online signatures. Proceedings of the 16th International Conference on Pattern Recognition (ICPR '02), 2002, Quebec, Canada 1: 123-126.
Feng H, Wah CC: Private key generation from on-line handwritten signatures. Information Management and Computer Security 2002, 10(4):159-164. 10.1108/09685220210436949
Chang Y-J, Zhang W, Chen T: Biometrics-based cryptographic key generation. Proceedings of the IEEE International Conference on Multimedia and Expo (ICME '01), June 2004, Taipei, Taiwan 3: 2203-2206.
Chen C, Veldhuis RNJ, Kevenaar TAM, Akkermans AHM: Multi-bits biometric string generation based on the likelihood ratio. Proceedings of the 1st IEEE International Conference on Biometrics: Theory, Applications, and Systems (BTAS '07), September 2007
Chen C, Veldhuis RNJ, Kevenaar TAM, Akkermans AHM: Biometric binary string generation with detection mate optimized bit allocation. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops (CVPR '08), June 2008
Chen C, Veldhuis RNJ, Kevenaar TAM, Akkermans AHM: Biometric quantization through detection rate optimized bit allocation. EURASIP Journal on Advances in Signal Processing 2009., 2009:
Chen C, Veldhuis RNJ: Extracting biometric binary strings with minimal area under the frr curve for the hamming distance classifier. Proceedings of the 17th European Signal Processing Conference (EUSIPCO '09), 2009
Chen C, Veldhuis R: Binary biometric representation through pairwise polar quantization. Proceedings of the 3rd International Conference on Advances in Biometrics (ICB '09), June 2009, Alghero, Italy, Lecture Notes in Computer Science 5558: 72-81.
Daugman J: The importance of being random: statistical principles of iris recognition. Pattern Recognition 2003, 36(2):279-291. 10.1016/S0031-3203(02)00030-4
Maio D, Maltoni D, Cappelli R, Wayman JL, Jain AK: FVC2000: fingerprint verification competition. IEEE Transactions on Pattern Analysis and Machine Intelligence 2002, 24(3):402-412. 10.1109/34.990140
Phillips PJ, Flynn PJ, Scruggs T, Bowyer KW, Chang J, Hoffman K, Marques J, Min J, Worek W: Overview of the face recognition grand challenge. Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR '05), June 2005, San Diego, Calif, USA 947-954.
Veldhuis R, Bazen A, Kauffman J, Hartel P: Biometric verification based on grip-pattern recognition. Security, Steganography, and Watermaking of Multimedia Contents VI, January 2004, San Jose, Calif, USA, Proceedings of SPIE 5306: 634-641.
Gardner M: The Binary Gray Code. W. H. Freeman, New York, NY, USA; 1986.
Acknowledgment
This research is supported by the research program Sentinels (http://www.sentinels.nl/). Sentinels is being financed by Technology Foundation STW, the Netherlands Organization for Scientific Research (NWO), and the Dutch Ministry of Economic Affairs.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, C., Veldhuis, R. Binary Biometric Representation through Pairwise Adaptive Phase Quantization. EURASIP J. on Info. Security 2011, 543106 (2011). https://doi.org/10.1155/2011/543106
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/543106





 ; (b)
; (b)  ; (c)
; (c)  , at various
, at various  locations:
locations:  . The detection rate ranges from 0 (black) to 1 (white).
. The detection rate ranges from 0 (black) to 1 (white).
 and
and  when the genuine user PDF
when the genuine user PDF  is modeled as with
is modeled as with  and four
and four  settings. The result is shown as (a) 1-bit APQ; (b) 2-bit APQ.
settings. The result is shown as (a) 1-bit APQ; (b) 2-bit APQ.
 of the 2-bit APQ to the 1-bit FQ (
of the 2-bit APQ to the 1-bit FQ ( ), when
), when  is modeled as (a)
is modeled as (a)  ; (b)
; (b)  , with various
, with various  locations:
locations:  . The detection rate ratio ranges from 1 (black) to 2 (white).
. The detection rate ratio ranges from 1 (black) to 2 (white).



 is modeled as
is modeled as  , with various
, with various  locations:
locations:  . The detection rate ratio scale is [1 2.2].
. The detection rate ratio scale is [1 2.2].
 ), computed from 50 feature pairs, for (a) FVC2000 and (b) FRGC.
), computed from 50 feature pairs, for (a) FVC2000 and (b) FRGC.
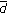 -
-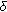 Property
Property
 , derived from the random pairing and the 2-bit APQ, for (a) FVC2000 and (b) FRGC.
, derived from the random pairing and the 2-bit APQ, for (a) FVC2000 and (b) FRGC.

 ; (b) the histogram of
; (b) the histogram of  for pairwise features and (c) an illustration of the pairwise features as independent Gaussian density, from both LS and random pairing.
for pairwise features and (c) an illustration of the pairwise features as independent Gaussian density, from both LS and random pairing.
 ) LS + APQ at various feature dimensionality D, as compared with the b/2-bit 1D FQ ( b-bit per feature pair), for (a) FVC2000, and (b) FRGC.
) LS + APQ at various feature dimensionality D, as compared with the b/2-bit 1D FQ ( b-bit per feature pair), for (a) FVC2000, and (b) FRGC.


 ; (c) the density of
; (c) the density of  ; (d) the pairwise phase density of
; (d) the pairwise phase density of  , with the adaptive quantization boundaries (dashed line).
, with the adaptive quantization boundaries (dashed line).