- Research Article
- Open access
- Published:
Peak-Shaped-Based Steganographic Technique for JPEG Images
EURASIP Journal on Information Security volume 2009, Article number: 382310 (2009)
Abstract
A novel model-based steganographic technique for JPEG images is proposed where the model, derived from heuristic assumptions about the shape of the DCT frequency histograms, is dependent on a stegokey. The secret message is embedded in DCT domain through an accurate selection of the potentially modifiable coefficients, taking into account their visual and statistical relevancy. A novel block measure, named discrepancy, is introduced in order to select suitable areas for embedding. The visual impact of the steganographic technique is evaluated through PSNR measures. State-of-the-art steganalytical test is also performed to offer a comparison with the original model-based techniques.
1. Introduction
Steganography is the art of hidden communication. Its aim is in fact to hide the presence of communication between two parties. Current steganographic techniques conceal secret messages in innocuous-looking data as images, audio files, and video files.
Following the approach in [1], the actual message to be transmitted is called embedded message, while the innocuous-looking message, in which the other will be enclosed, is the cover message (cover image in case of images). This embedding process creates a new message, called stego message (stego image in case of images), with the same visual and statistical appearance of the cover message but containing the embedded message.
Modern steganographic techniques follow Kerckhoffs' principle: the technique used to hide the embedded message is known to the opponent, and the security of the stegosystem lies only in the choice of a hidden information shared between the sender and the receiver, called stegokey [1].
Because of their large diffusion among the Internet, JPEG images are very attractive as cover messages. As a consequence, many steganographic techniques have been designed for JPEG, most of them embedding the message in DCT domain by modifying the least significant bits (LSBs) of the quantized DCT coefficients. One of the first JPEG steganographic techniques following this approach is Jsteg [2]. Outguess [3] is not only similar to Jsteg, but also preserves DCT global histogram by additional bit-flipping. F5 [2] performs the embedding by decreasing the absolute value of DCT coefficients, thus preserving the DCT histograms peak-shape. Unfortunately, all the techniques are detected with known statistical methods [4].
Model-based steganography (MB) [5] introduces a different methodology, where the message is embedded in the cover according to a model representing cover message statistics. In [5], two image steganographic techniques (MB1 and MB2) are illustrated: MB1 models DCT AC histograms by the generalized Cauchy distribution and embeds the message in the cover image through an entropy decoder driven by the model. MB2 also preserves blockiness [6]. In [7], an ad hoc steganalytical test is developed to detect MB1.
The aim of this work is to improve the performance of the mentioned Model-based techniques by considering a better model and a more accurate selection of the modifiable coefficients. The peak-shaped-based (PSB) technique, here illustrated, applies F5 heuristic principles in a Model-based methodology. It is known that both MB1 and MB2 modeling of every DCT AC frequency leaves a fingerprint which allows to detect the presence of the embedded message. In fact, MB1 is detected via a model calculation followed by a goodness-of-fit test [7]. On the other hand, PSB modeling does not characterize strictly DCT AC histograms, but only models in a broad sense the histograms shape. Many cover images already present similar properties, thus making much more difficult the fingerprint discovering. Moreover, PSB model depends on the stegokey: a simple analysis of the stego image is not sufficient to perform an exact model calculation, regardless of the possible attacker. Futhermore, PSB accurately selects the modifiable coefficients by exploiting the quantization matrix and introducing a novel parameter, named discrepancy, measuring how much a given image portion is suitable for embedding the hidden message.
This paper is organized as follows. Model-based methodology is introduced in Section 2, together with embedding and extraction algorithms. In Section 3 the PSB technique is described and its superior performance over original Model-based techniques is demonstrated. Conclusions are drawn in Section 4.
2. PSB Steganography
The steganographic technique introduced in this work, named peak-shaped-based steganography (PSB), is developed following the Model-based steganography principles exposed in Sallee's work [5] of which for sake of completeness, a brief outline is given in Section 2.1. Next, PSB is illustrated and the embedding and the extraction algorithm are described.
2.1. Principles of Model-Based Steganography
Model-based steganography was first introduced in 2003 [5]. The aim of Model-based steganography is in characterizing some statistical properties of the cover message in order to embed the secret message without altering these properties. The outline of Model-based steganography is described in the following.
A cover message, represented as a random variable  , is split into two parts,
, is split into two parts,  , that remain unaltered during the embedding, and
, that remain unaltered during the embedding, and  , that is modified to carry the embedded message.
, that is modified to carry the embedded message.  is selected so as to preserve the relevant characteristics of the cover, whereas
is selected so as to preserve the relevant characteristics of the cover, whereas  can be modified without altering the perceptual and statistical characteristics of the cover message. By modeling the cover message class
can be modified without altering the perceptual and statistical characteristics of the cover message. By modeling the cover message class  according to a probability distribution
according to a probability distribution  it is possible to calculate the conditioned probability distribution
it is possible to calculate the conditioned probability distribution  .
.
The embedded message is assumed to be a uniform random stream of bits, which is in fact the same distribution shown by encrypted messages. The embedding outline is shown in Figure 1. The cover message  is split into
is split into  and
and  , then the embedded message is processed by an entropy decoder according to the conditioned probability distribution
, then the embedded message is processed by an entropy decoder according to the conditioned probability distribution  . The output of the decoder is denoted by
. The output of the decoder is denoted by  and replaces
and replaces  to form together with
to form together with  the stego message
the stego message  .
.
The extraction outline is shown in Figure 2. Its structure is very similar to the embedding scheme: the main difference consists in the replacement of the entropy decoder by an entropy encoder. The stego message  is separated in
is separated in  and
and  . The conditioned probability distribution
. The conditioned probability distribution  is calculated, then the entropy encoder process
is calculated, then the entropy encoder process  according to the model distribution. The encoder output is the embedded message.
according to the model distribution. The encoder output is the embedded message.
From now on, since the main focus of this work is on hiding information in images, the cover messages will be denoted as cover images.
2.2. Selection of the Modifiable Coefficient Set
The JPEG compression codes the images by dividing them in blocks, calculating DCT coefficients for every block, and then performing a coefficient quantization. Thus, the quantization makes it impossible to get the original image after the compression. This is an issue for steganography, since hiding the message in the spatial domain should take into account this information loss. Instead, embedding the message in DCT domain permits to avoid this issue. Hence,  is selected as a subset of quantized DCT coefficients. The modifiable coefficients are accurately selected in order to preserve the visual and the statistical characteristics of the cover image. The selection consists in three steps: in the first step a preliminary coefficient exclusion is performed, in the second step the maximum number of modifiable coefficients per block is calculated, and then in the final step the modifiable coefficients are selected.
is selected as a subset of quantized DCT coefficients. The modifiable coefficients are accurately selected in order to preserve the visual and the statistical characteristics of the cover image. The selection consists in three steps: in the first step a preliminary coefficient exclusion is performed, in the second step the maximum number of modifiable coefficients per block is calculated, and then in the final step the modifiable coefficients are selected.
2.2.1. Preliminary Coefficients Exclusion
At first, some of the coefficients are excluded from embedding because of their visual or statistical relevance. This set includes
(i)DC coefficients;
(ii)zero-valued coefficients;
(iii)highly quantized DCT frequencies;
(iv)unitary coefficients.
DC coefficients are excluded from embedding because of their visual relevance, since they represent the mean luminance value of a block. Zero-valued coefficients are also excluded, since they occur in featureless areas of the image where changes are most likely to create visible artefacts. All the highly quantized DCT frequencies (whose quantization coefficients are greater of a threshold  ) are discarded during the embedding because small changes in these coefficients result in large alterations in the respective dequantized coefficients. Moreover, unitary coefficients
) are discarded during the embedding because small changes in these coefficients result in large alterations in the respective dequantized coefficients. Moreover, unitary coefficients  are also excluded from embedding; experimental results illustrated in Section 3.2.3 show that modifying unitary coefficients increases detectability.
are also excluded from embedding; experimental results illustrated in Section 3.2.3 show that modifying unitary coefficients increases detectability.
The residual coefficient set is denoted by  . Moreover, for every block
. Moreover, for every block  , let
, let  denote the number of remaining coefficients in the block.
denote the number of remaining coefficients in the block.
2.2.2. Coefficient Modification
Every DCT coefficient, according to its value, is represented by a group and an offset. Denoting  the DCT coefficient, its group
the DCT coefficient, its group  is calculated through the following expression:
is calculated through the following expression:

Thus all the groups are disjoint and have two elements which differ only in one unitary value, for example,  , and so forth.
, and so forth.
The coefficient offset  is defined by the following expression:
is defined by the following expression:

thus offsets can be only 1 or 2. PSB embeds the message by changing modifiable coefficient offsets, thus only unitary increments/decrements are possible, for example, a coefficient whose value is  , after embedding could be only 2 or 3 (its group is
, after embedding could be only 2 or 3 (its group is  ). Offsets are modified according to the model.
). Offsets are modified according to the model.
2.2.3. Discrepancy
Some areas of the image could not be suitable to embed the message (e.g., a periodic texture, a sharp area, and so forth where changes could be more detectable), but a first-order statistic modeling is not able to discriminate such areas. A new measure is introduced, named discrepancy, to derive the embedding suitability of an area. The discrepancy is calculated at block layer and expresses how much a block is similar to adjacent blocks. In PSB, discrepancy is used to determine the maximum number of modifiable coefficients within a block.
Block  discrepancy is an approximation of the mean value of the
discrepancy is an approximation of the mean value of the  -distance, calculated in DCT domain, between block
-distance, calculated in DCT domain, between block  and block
and block  , where
, where  is one of the blocks shown in Figure 3:
is one of the blocks shown in Figure 3:

being  the discrepancy,
the discrepancy,  the quantization coefficient of the i th DCT frequency.
the quantization coefficient of the i th DCT frequency.  assumes the following expression:
assumes the following expression:

where  is
is  th quantized DCT coefficient of
th quantized DCT coefficient of  th block. Since the embedding modifies the exact
th block. Since the embedding modifies the exact  -distances from the blocks, and the sender, and the receiver must calculate the same discrepancy in order to extract the embedded message, discrepancy is not calculated as the exact mean, thus the approximation (3) is required. If the block
-distances from the blocks, and the sender, and the receiver must calculate the same discrepancy in order to extract the embedded message, discrepancy is not calculated as the exact mean, thus the approximation (3) is required. If the block  is on image border the discrepancy is calculated taking into account only existing blocks.
is on image border the discrepancy is calculated taking into account only existing blocks.
Since discrepancy is larger when blocks are different, a block is suitable for embedding when it has a large discrepancy. Numerical simulations show that the discrepancy calculated in random pixel images is 4284 on average. Assuming that steganography works better on random pixel images, PSB divides the interval  in 63 subintervals labeled from 0 to 62:
in 63 subintervals labeled from 0 to 62:  is 0,
is 0,  is
is  is 62, and
is 62, and  is 63. Let
is 63. Let  denote the label from block
denote the label from block  then
then

 represents the maximum number of modifiable coefficients for block
represents the maximum number of modifiable coefficients for block  according to discrepancy, but without considering the preliminary exclusions illustrated in Section 2.2.1. Therefore the actual maximum number of modifiable coefficients for block
according to discrepancy, but without considering the preliminary exclusions illustrated in Section 2.2.1. Therefore the actual maximum number of modifiable coefficients for block  ,
,  , is calculated through the following expression:
, is calculated through the following expression:

If  the coefficients are selected from
the coefficients are selected from  by a pseudo random noise generator (PRNG) seeded by the stegokey.
by a pseudo random noise generator (PRNG) seeded by the stegokey.
The class of the remaining coefficients after the random selection is denoted by  . (Even if
. (Even if  should represent the class of the remaining coefficients offsets, to lighten the notation it will denote the entire coefficients.)
should represent the class of the remaining coefficients offsets, to lighten the notation it will denote the entire coefficients.)
2.3. Message Embedding
The offsets of the coefficients belonging to  are replaced according to the message and the model described in the next sections.
are replaced according to the message and the model described in the next sections.
2.3.1. Coefficient Permutation
The embedded message is scattered across the image using a PRNG seeded by the stegokey that permutes the order of the modifiable coefficients. As reported in [2], it represents a good solution to spread the embedded message in the whole image, both in spatial and in DCT domains.
2.3.2. The Peak-Shaped Model
The peak-shaped model is a first-order model characterizing DCT frequency histograms. The model is dependent on the stegokey and therefore an attacker is not able to calculate it exactly.
The model is based on two heuristic assumption derived from F5 steganography [2]:

being  the histogram of a fixed DCT AC frequency and
the histogram of a fixed DCT AC frequency and  a positive DCT coefficient. Similar properties apply on negative coefficients. For sake of simplicity the model is described only for positive coefficients on a fixed DCT AC frequency, but equivalent steps hold also from negative coefficients and all the DCT AC frequencies.
a positive DCT coefficient. Similar properties apply on negative coefficients. For sake of simplicity the model is described only for positive coefficients on a fixed DCT AC frequency, but equivalent steps hold also from negative coefficients and all the DCT AC frequencies.
The peak-shaped model characterizes offset probabilities for the groups by exploiting (7). Let  denote the stego image histogram (for a fixed DCT AC frequency) and
denote the stego image histogram (for a fixed DCT AC frequency) and  a coefficient group:
a coefficient group:

where  is the first offset probability conditioned to group
is the first offset probability conditioned to group  . Let
. Let  denote the group histogram and assuming
denote the group histogram and assuming  , then (7) leads to
, then (7) leads to

Defining  , the stego image histogram is
, the stego image histogram is

From (7) and (10), the simple algebra calculations lead to


By exploiting (11) and (12) it is possible to find an iterative algorithm to obtain  . However, (11) and (12) are not always satisfied in conjunction, but only when
. However, (11) and (12) are not always satisfied in conjunction, but only when

Finally,  is calculated recursively starting with the largest group
is calculated recursively starting with the largest group  following the algorithm illustrated by the flow chart in Figure 4.
following the algorithm illustrated by the flow chart in Figure 4.
-
(i)
For
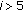 ,
,  since large coefficients are not statistically relevant [8]. Moreover, Figure 5 shows the deviation of the offset distribution per group from a uniform offset distribution at the DCT frequency
since large coefficients are not statistically relevant [8]. Moreover, Figure 5 shows the deviation of the offset distribution per group from a uniform offset distribution at the DCT frequency  averaged on an image database: groups with
averaged on an image database: groups with 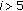 show a little deviation from the uniform distribution. In addition, it maximizes the embedding capacity for these groups.
show a little deviation from the uniform distribution. In addition, it maximizes the embedding capacity for these groups. -
(ii)
For
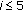 if
if 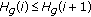 or
or 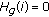 then
then  . If (13) is not satisfied, the inferior limit expressed by (11) is assumed to be 0.
. If (13) is not satisfied, the inferior limit expressed by (11) is assumed to be 0.  is derived by a PRNG (pseudo random noise generator) seeded by the stegokey according to (11) and (12).
is derived by a PRNG (pseudo random noise generator) seeded by the stegokey according to (11) and (12).
2.4. Algorithm Summary
A summary of the embedding and the extraction algorithm is illustrated in the following.
2.4.1. Embedding Outline
The embedding algorithm follows the steps listed as follows:
-
(i)
a header is added to the embedded message: the header is formed by two parts, one of fixed length (5 bits) and one of variable length, whose dimension is written in the fixed part. Message length is written into the variable part;
-
(ii)
a preliminary exclusion of non-modifiable coefficients (as described in Section 2.2.1) is performed and
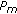 is calculated for every block
is calculated for every block 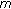 ;
; -
(iii)
discrepancy is calculated according to (3), and
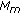 is derived for every block
is derived for every block 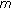 ;
; -
(iv)
the maximum number of modifiable coefficients per block is calculated through (6);
(v)  is derived by selection of the modifiable coefficients for each block using PRNG if
is derived by selection of the modifiable coefficients for each block using PRNG if  ;
;
-
(vi)
a permutation of modifiable coefficients is performed by the PRNG;
-
(vii)
the offset probabilities are calculated for every modifiable coefficient according to the model;
-
(viii)
the embedded message is processed by the arithmetic decoder illustrated in [5, 9] according to the order established above;
-
(ix)
the modifiable coefficient offsets are replaced by the output of the arithmetic decoder.
2.4.2. Extraction Outline
The extraction algorithm follows the steps listed as follows:
-
(i)
a preliminary exclusion of non-modifiable coefficients (as described in Section 2.2.1) is performed, and
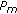 is calculated for every block
is calculated for every block 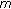 ;
; -
(ii)
discrepancy is calculated according to (3), and
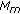 is derived for every block
is derived for every block 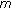 ;
; -
(iii)
the maximum number of modifiable coefficients is calculated through (6);
(iv)  is derived by selection of the modifiable coefficients for each block using PRNG if
is derived by selection of the modifiable coefficients for each block using PRNG if  ;
;
-
(v)
a permutation of modifiable coefficients is performed by the PRNG;
-
(vi)
the offset probabilities are calculated for every modifiable coefficient according to the model;
-
(vii)
the message is obtained by encoding the offsets using the arithmetic encoder [5, 9];
-
(viii)
the header is inspected so as to read the message length and to extract the message.
2.5. Embedding Capacity
Embedding capacity is defined as the maximum mean message length which could be embedded in an image.
A modifiable coefficient  can hold as many bits as the entropy of the binary alphabet associated to its group
can hold as many bits as the entropy of the binary alphabet associated to its group  :
:

where  is the probability of the first offset conditioned to group
is the probability of the first offset conditioned to group  . So the embedding capacity is
. So the embedding capacity is

3. Experimental Results
To test the validity of this technique, PSB is compared to the original Model-based steganography (MB1 and MB2, described in [5]). Two experiments are performed: in the first experiment the visual degradation in the image introduced by the steganography is evaluated by calculating PSNR; in the second experiment the state-of-the-art steganalytical test [10] is performed to compare the robustness of the techniques.
These test are carried out on an image database that contains 2000 images taken from BOWS-2 database [11]. All the images are natively in lossless format and gray-scaled. Image dimensions are  pixels. The images are converted in JPEG format with a fixed quality factor equal to 80.
pixels. The images are converted in JPEG format with a fixed quality factor equal to 80.
3.1. PSNR Evaluation
This experiment is performed by embedding the same message for the three techniques and then evaluating PSNR. The message length is different among the images and equals to the PSB embedding capacity, which is the smallest among the techniques, because of PSB unitary coefficients exclusion. PSNR results are shown in Table 1: PSB achieves slightly higher PSNR with respect to MB1 and MB2 (0.5 dB higher); moreover PSNR is adequate to ignore the visual degradation introduced by the three techniques. The degradation introduced by MB2 blockiness compensation is negligible.
3.2. Steganalytical Test
PSB detectability is compared to MB1 and MB2 by means of the state-of-the-art steganalytical test [10].
3.2.1. Test Overview
Following [10] the evaluation is performed as follows:
-
(i)
the image database is split in a training set (1300 images) and a testing set (700 images);
-
(ii)
the embedded message is the same for all the three techniques but it differs among the images. The message length for a given image is set as a fixed percentage of the image nonzero AC DCT coefficients (bpac-bit per nonzero AC coefficient). The following [10] experiments are performed at 0.05, 0.1, 0.15, 0.2 bpac;
-
(iii)
no header is added to the message since it is negligible for the aim of the test;
-
(iv)
both the test images and the train images are analyzed by the steganalyzer without the embedded message (as cover images) and with the embedded message (as stego images);
-
(v)
the support vector machine (SVM) [12, 13] is trained with the features of the training set scaled in
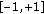 ;
; -
(vi)
the SVM parameters
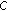 and
and 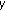 are estimated by a five-fold cross-validation.
are estimated by a five-fold cross-validation.
The simulation outcome is expressed by the error probability  that is the minimal total average error probability [10] on the testing set:
that is the minimal total average error probability [10] on the testing set:

where  and
and  are the probability of false alarm and missed detection, respectively. The aim of a steganographic technique is in achieving a high error probability.
are the probability of false alarm and missed detection, respectively. The aim of a steganographic technique is in achieving a high error probability.
3.2.2. PSB Steganalysis
Figure 6 shows test results: it is noticeable that PSB outperforms MB1 and MB2 at every bpac. Indeed, PSB error probability is about 0.13 higher than MB1 error probability. At 0.05 bpac PSB achieves about 0.35 error probability whereas MB1 and MB2 error probabilities are about 0.22. At higher bpac, all the techniques get lower error probabilities: at 0.2 bpac MB1 and MB2 are always detected, in fact the both get 0.008 error probability, instead of PSB error probability which is near 0.07.
Figure 7 shows the embedding impact as the mean (among the images) of the ratio between the number of modified coefficients and the total number of nonzero AC coefficients. PSB replaces a few more coefficients than MB1 but it gets lower visual degradation and larger error probability. Moreover MB2 has the major embedding impact on AC coefficients due to the addictional changes to preserve blockiness.
By comparing the embedding impact to the error probability and PSNR it results that the embedding impact has a minor relevance with respect to the selection of the modifiable coefficients. In fact, PSB outperforms MB1 in error probability and gets similar PSNR with a larger embedding impact. These superior performances are achieved by taking into account discrepancy and quantization matrix in order to select the modifiable coefficients set. MB2 modifies additional coefficients to preserve a superior-order statistical measure, but the additional coefficients to be replaced are not selected carefully, getting the worst performances.
3.2.3. Unitary Coefficient Exclusion
Since unitary coefficients are the most common coefficient values except for 0, their exclusion affects embedding capacity, but on the other hand modifying unitary coefficients increases detectability. In fact, Table 2 shows error probability for a modified PSB including unitary coefficient values, denoted by PSB+1 (groups and model are modified to include unitary coefficient values). PSB and MB1 are also included for sake of readability. It can be seen that unitary coefficient values exclusion increases PSB error probability by approximately 0.04 at bpac minor than 0.2, motivating their exclusion. At bpac larger than 0.2 both PSB, MB1 and PSB+1 get a zero error probability, hence it no longer makes sense the embedding. Therefore, the unitary coefficient values impact on embedding capacity is negligible.
Moreover, Table 3 shows the embedding impact of PSB+1 with respect to PSB. Both the techniques achieve the same embedding impact, whereas PSB+1 gets lower error probability. This is a further confirm to the minor relevance of the embedding impact with respect to the selection of suitable coefficients.
3.2.4. Error Probability at Different Quality Factors
Usually JPEG quality factors used in storage are included in the interval  that is a good trade-off between quality and file size. Hence in the previous experiments the quality factor is set to 80. Moreover, in [8] the quality factor is set to 80, whereas in [10] and in [4] is set, respectively, to 75 and 70. Although the quality factor choice is arbitrary, the steganographic detectability could be affected by the different quantization, so some experiments are made to test PSB detectability with different quality factor. The results are illustrated in Table 4. PSB outperforms MB1 and MB2 at all the quality factors. Furthermore, PSB error probability, together with MB1 and MB2 error probability, is affected only partially by the quality factor. In fact at 0.05 bpac the error probabilities at the two quality factors differ only in 0.03, whereas at 0.1 bpac the error probabilities are the same. MB1 and MB2 show a larger difference, in particular MB2 error probabilities at 0.05 bpac differ in 0.07. Interesting enough, PSB undetectability improves at the quality factor increase, instead of MB1 and MB2 that show the opposite behavior.
that is a good trade-off between quality and file size. Hence in the previous experiments the quality factor is set to 80. Moreover, in [8] the quality factor is set to 80, whereas in [10] and in [4] is set, respectively, to 75 and 70. Although the quality factor choice is arbitrary, the steganographic detectability could be affected by the different quantization, so some experiments are made to test PSB detectability with different quality factor. The results are illustrated in Table 4. PSB outperforms MB1 and MB2 at all the quality factors. Furthermore, PSB error probability, together with MB1 and MB2 error probability, is affected only partially by the quality factor. In fact at 0.05 bpac the error probabilities at the two quality factors differ only in 0.03, whereas at 0.1 bpac the error probabilities are the same. MB1 and MB2 show a larger difference, in particular MB2 error probabilities at 0.05 bpac differ in 0.07. Interesting enough, PSB undetectability improves at the quality factor increase, instead of MB1 and MB2 that show the opposite behavior.
4. Conclusions
A new Model-based technique, named peak-shaped-based steganography, is introduced in order to improve the original Model-based steganography. PSB novelty is in a more accurate coefficient selection, taking into account quantization and coefficient relevancy. A novel block measure, named discrepancy, is introduced to describe how much a block is suitable to embed a message. PSB model derives from heuristic hypothesis about histogram shape, moreover the model depends on the stegokey, therefore an attacker cannot calculate exactly the model. The message is scattered in the image by a PRNG seeded by the stegokey. The technique is evaluated by calculating the PSNR on an image database and performing the state-of-the-art steganalytical test described in [10]. In each test PSB outperforms the original Model-based techniques. It is also shown that the embedding impact (how many coefficients are modified during the embedding) results having minor relevance with respect to the selection of the areas in which the message is embedded.
Future work on JPEG steganography are directed toward a superior-order modeling of the DCT coefficients, by studying Markov Random Fields and the effect of image noise in DCT domain. In particular, since unitary coefficients modification affects detectability, they are actually excluded from the embedding. However, their exclusion decreases embedding capacity. The authors believe that if a more accurate model is used, unitary coefficients could be included to increase the capacity with no detectability increase.
References
Anderson RJ, Petitcolas FAP: On the limits of steganography. IEEE Journal of Selected Area in Communications 1998, 16(4):474-481. 10.1109/49.668971
Westfeld A: F5—a steganographic algorithm. Proceedings of the 4th International Workshop on Information Hiding (IH '01), April 2001, Pittsburgh, Pa, USA, Lecture Notes in Computer Science 2137: 289-302.
Provos N: Defending against statistical steganalysis. Proceedings of the 10th USENIX Security Symposium, August 2001, Washington, DC, USA 323-335.
Fridrich J, Pevný T, Kodovský J: Statistically undetectable JPEG steganography: dead ends challenges, and opportunities. Proceedings of the 9th Workshop on Multimedia & Security (MM&Sec '07), September 2007, Dallas, Tex, USA 3-14.
Sallee P: Model-based steganography. Proceedings of the International Workshop on Digital Watermarking (IWDW '03), October 2003, Seoul, Korea 154-167.
Fridrich J, Goljan M, Hogea D: Attacking the outguess. Proceedings of the 10th ACM Workshop on Multimedia & Security (MM&Sec '02), December 2002, Juan-les-Pins, France 3-6.
Böhme R, Westfeld A: Breaking Cauchy model-based JPEG steganography with first order statistics. Proceedings of the 9th European Symposium on Research in Computer Security (ESORICS '04), September 2004, Sophia Antipolis, France 125-140.
Fridrich J: Feature-based steganalysis for JPEG images and its implications for future design of steganographic schemes. Proceedings of the 6th International Workshop on Information Hiding (IH '04), May 2004, Toronto, Canada 67-81.
Witten I, Neal R, Clearly J: Arithmetic coding for data compression. Communications of the ACM 1987, 30(6):520-540. 10.1145/214762.214771
Fridrich J, Pevny T: Merging Markov and DCT features for multi-class JPEG steganalysis. Security, Steganography, and Watermarking of Multimedia Contents IX, January 2007, San Jose, Calif, USA, Proceedings SPIE 6505: 3-4.
BOWS-2 database (clean images) http://dud.inf.tu-dresden.de/~westfeld/rsp/
Chang C, Lin CLIBSVM: a library for support vector machines, Software, 2001, http://www.csie.ntu.edu.tw/~cjlin/libsvm/
Hsu C, Chang C, Lin C: A Practical Guide to Support Vector Classification. 2007, http://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf
Acknowledgment
The authors would like to thank Patrick Bas and Teddy Furon for making the BOWS-2 database available.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Rossi, L., Garzia, F. & Cusani, R. Peak-Shaped-Based Steganographic Technique for JPEG Images. EURASIP J. on Info. Security 2009, 382310 (2009). https://doi.org/10.1155/2009/382310
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/382310




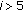 ,
,  since large coefficients are not statistically relevant [
since large coefficients are not statistically relevant [ averaged on an image database: groups with
averaged on an image database: groups with 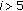 show a little deviation from the uniform distribution. In addition, it maximizes the embedding capacity for these groups.
show a little deviation from the uniform distribution. In addition, it maximizes the embedding capacity for these groups.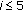 if
if 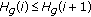 or
or 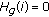 then
then  . If (13) is not satisfied, the inferior limit expressed by (11) is assumed to be 0.
. If (13) is not satisfied, the inferior limit expressed by (11) is assumed to be 0.  is derived by a PRNG (pseudo random noise generator) seeded by the stegokey according to (11) and (12).
is derived by a PRNG (pseudo random noise generator) seeded by the stegokey according to (11) and (12).
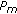 is calculated for every block
is calculated for every block 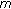 ;
;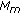 is derived for every block
is derived for every block 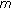 ;
;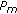 is calculated for every block
is calculated for every block 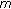 ;
;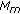 is derived for every block
is derived for every block 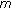 ;
;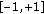 ;
;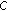 and
and 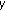 are estimated by a five-fold cross-validation.
are estimated by a five-fold cross-validation.
