- Research Article
- Open access
- Published:
Steganography in 3D Geometries and Images by Adjacent Bin Mapping
EURASIP Journal on Information Security volume 2009, Article number: 317165 (2009)
Abstract
A steganographic method called adjacent bin mapping (ABM) is presented. Firstly, it is applied to 3D geometries by mapping the coordinates within two adjacent bins for data embedding. When applied to digital images, it becomes a kind of LSB hiding, namely the  algorithm. In order to prevent the detection using a metric named histogram tail, the hiding is performed in a pseudorandom order. Then we show that the steganalytic algorithms based on histogram characteristic function (HCF) can be prevented by implementing the
algorithm. In order to prevent the detection using a metric named histogram tail, the hiding is performed in a pseudorandom order. Then we show that the steganalytic algorithms based on histogram characteristic function (HCF) can be prevented by implementing the  algorithm on subsets of pixels having the same neighbor values. The experimental results show that important high-order statistics of the cover image are preserved in this way while little distortion is introduced to 3D geometric models with an appropriate bin size.
algorithm on subsets of pixels having the same neighbor values. The experimental results show that important high-order statistics of the cover image are preserved in this way while little distortion is introduced to 3D geometric models with an appropriate bin size.
1. Introduction
Steganography, the art of covert communication by hiding the presence of a message typically in multimedia content, has attracted the interests of researchers (e.g., [1–4]). Although the early steganographic methods can imperceptibly embed data into a cover object, traces of data embedding can be found within the characteristics of the stego objects. In the last decade, the technique of steganalysis (e.g., [5]) has been developed for the detection of hidden data. It has been shown by the novel steganalytic algorithms and detection-theoretic analysis that several hiding methods are detectable. Therefore, how to prevent the hidden message from being detected is a central topic of steganography research.
Most of the steganalytic algorithms (e.g., [6–21]) exploit statistical characteristics of the stego objects to detect the existence of hidden message. For instance, the  (chi-squared) technique [6] and Provos' stegdetect [7] calculate the number of pixels whose values differ only in the least significant bit (LSB) to detect random LSB hiding. Furthermore, the occurrence of a pair of spatially adjacent pixels is counted for steganalysis of random LSB hiding in the regular/singular (RS) scheme [8] and more theoretical sample pair analysis (SPA) [9]. By modeling the hiding process as additive noise, histogram characteristic function (HCF) is introduced in [10] to detect LSB, spread spectrum, and discrete cosine transform (DCT) hiding methods. Two ways of applying HCF are further proposed in [11] to detect the LSB matching steganography in gray-scale images. The detection-theoretic analysis for steganalysis can be found in [12, 13] for the block-based embedding in the Gaussian random covers and by modeling the cover as a Markov chain, respectively. Moreover, features such as image quality metrics [14] and the high-order statistics [15–17] are used through supervised learning to detect the arbitrary hiding scheme.
(chi-squared) technique [6] and Provos' stegdetect [7] calculate the number of pixels whose values differ only in the least significant bit (LSB) to detect random LSB hiding. Furthermore, the occurrence of a pair of spatially adjacent pixels is counted for steganalysis of random LSB hiding in the regular/singular (RS) scheme [8] and more theoretical sample pair analysis (SPA) [9]. By modeling the hiding process as additive noise, histogram characteristic function (HCF) is introduced in [10] to detect LSB, spread spectrum, and discrete cosine transform (DCT) hiding methods. Two ways of applying HCF are further proposed in [11] to detect the LSB matching steganography in gray-scale images. The detection-theoretic analysis for steganalysis can be found in [12, 13] for the block-based embedding in the Gaussian random covers and by modeling the cover as a Markov chain, respectively. Moreover, features such as image quality metrics [14] and the high-order statistics [15–17] are used through supervised learning to detect the arbitrary hiding scheme.
To avoid being detected by the steganalytic algorithms, quite a few algorithms are designed to preserve the statistics of the cover object. An early attempt is the F5 algorithm [22], in which some characteristics in the histogram of DCT coefficients are preserved to prevent  attack [6]. However, it is broken by the detector designed by Fridrich et al. [18] by estimating the cover histogram from the suspected image for comparison. In Provos' Outguess [23], part of JPEG coefficients are used to repair the modified histogram due to data embedding. But the changes at the block boundaries can be used for detection because the embedding is performed in the blockwise transform domain [19]. A method attempting to preserve the histogram after LSB hiding is further presented by Franz [24], where a message that mimics the imbalance between the adjacent histogram bins is embedded. But the asymmetric embedding process determined by a cooccurrence matrix can be exploited for steganalytic attack, as shown in [20]. Similarly, Eggers et al. propose a histogram-preserving data-mapping (HPDM) method [25] by embedding a message with the same distribution as the cover object. However, it is shown by Tzschoppe et al. [26] that HPDM can be detected by Lyu and Farid's steganalytic method [15] because higher-frequency components have not been separately treated from lower-frequency ones. So a histogram restoration algorithm is proposed in [27] without embedding in the low-probability region, and further adopted to preserve some second-order statistics in [28].
attack [6]. However, it is broken by the detector designed by Fridrich et al. [18] by estimating the cover histogram from the suspected image for comparison. In Provos' Outguess [23], part of JPEG coefficients are used to repair the modified histogram due to data embedding. But the changes at the block boundaries can be used for detection because the embedding is performed in the blockwise transform domain [19]. A method attempting to preserve the histogram after LSB hiding is further presented by Franz [24], where a message that mimics the imbalance between the adjacent histogram bins is embedded. But the asymmetric embedding process determined by a cooccurrence matrix can be exploited for steganalytic attack, as shown in [20]. Similarly, Eggers et al. propose a histogram-preserving data-mapping (HPDM) method [25] by embedding a message with the same distribution as the cover object. However, it is shown by Tzschoppe et al. [26] that HPDM can be detected by Lyu and Farid's steganalytic method [15] because higher-frequency components have not been separately treated from lower-frequency ones. So a histogram restoration algorithm is proposed in [27] without embedding in the low-probability region, and further adopted to preserve some second-order statistics in [28].
The model-based steganography [29] provides a new perspective by generating a stego object with a given distribution model. However, due to the lack of a perfect model, the steganographic algorithm using generalized Cauchy distribution can be broken by using the first-order statistics, that is, the measures without considering the interdependencies between observations, such as mean and variance [21]. In our preliminary work [30], a new steganographic method is proposed to preserve the marginal distribution of a cover inherently, which is called adjacent bin mapping (ABM) hereinafter. In this paper, we apply ABM method to three-dimensional (3D) geometric models by mapping the coordinates within two adjacent bins for data embedding. When applied to digital images, it becomes a sort of LSB hiding, namely, the  algorithm. For image steganography, we analyze one case that the
algorithm. For image steganography, we analyze one case that the  algorithm is detectable by defining a high-order metric named histogram tail. And we try to prevent the detection by performing the hiding in a pseudorandom order. To prevent SPA steganalysis [9], the
algorithm is detectable by defining a high-order metric named histogram tail. And we try to prevent the detection by performing the hiding in a pseudorandom order. To prevent SPA steganalysis [9], the  algorithm has been implemented on subsets of pixels having the same four neighbor values (left, right, up, and down), as shown in [30]. In this paper, we show that the steganalytic algorithms in [11] to detect LSB matching steganography can be prevented by performing the
algorithm has been implemented on subsets of pixels having the same four neighbor values (left, right, up, and down), as shown in [30]. In this paper, we show that the steganalytic algorithms in [11] to detect LSB matching steganography can be prevented by performing the  algorithm on subsets of pixels having the same five neighbor values (i.e., left, right, up, down, and up-right, denoted by 5-N in short). The experimental results show that several important statistics of a cover image are preserved in this way, while little distortion is introduced to the virtual reality modeling language (VRML) models with an appropriate bin size.
algorithm on subsets of pixels having the same five neighbor values (i.e., left, right, up, down, and up-right, denoted by 5-N in short). The experimental results show that several important statistics of a cover image are preserved in this way, while little distortion is introduced to the virtual reality modeling language (VRML) models with an appropriate bin size.
The rest of this paper is organized as follows. In the next section, the ABM method is reviewed, and its application to geometry steganography is proposed. In Section 3, the  algorithm is presented, and we try to prevent the histogram tail detection and the steganalytic algorithms based on HCF, respectively. The experimental results are given in Section 4. Finally, a conclusion is drawn in Section 5.
algorithm is presented, and we try to prevent the histogram tail detection and the steganalytic algorithms based on HCF, respectively. The experimental results are given in Section 4. Finally, a conclusion is drawn in Section 5.
2. Adjacent Bin Mapping for Steganography
In this section, the data mapping method proposed in [30] is reviewed, which is called adjacent bin mapping (ABM) hereinafter. One important property of the ABM method is that it preserves the marginal distribution of a cover inherently. Other properties include the applicability to a variety of cover objects (e.g., represented by integers, floating or fixed point numbers) as well as the relative simplicity of both encoding and decoding.
2.1. The Adjacent Bin Mapping Method
Different from other embedding methods, the ABM method does not generate new values in the stego object. Instead, the elements in two adjacent bins are mapped to each other for data embedding. In other words, we can say that the elements in the original object are bijectively mapped to those in the stego object. Suppose a cover object  consists of
consists of  elements, that is,
elements, that is,  , where
, where  is an element with the index number
is an element with the index number  . We use
. We use  to denote the distribution range of the elements
to denote the distribution range of the elements  and divide
and divide  into nonoverlapping bins with the same size
into nonoverlapping bins with the same size  . For the sake of simplicity, we only discuss the one-dimensional case because multiple dimensions can be processed one by one. As shown in Figure 1, every two adjacent bins in the range of
. For the sake of simplicity, we only discuss the one-dimensional case because multiple dimensions can be processed one by one. As shown in Figure 1, every two adjacent bins in the range of  form an embedding unit, within which the bit values 0 and 1 are assigned to the left and right bins, respectively. If the value of an element
form an embedding unit, within which the bit values 0 and 1 are assigned to the left and right bins, respectively. If the value of an element  falls into the left bin, it represents a bit value of 0, otherwise 1 if it is in the right bin. To embed a bit value of 0, an element should be kept in the left bin if it was originally the case, or moved to the left bin if it originally was in the right one. The process to embed a bit value of 1 is similar as long as we replace "left" by "right" and vice versa. The key idea of the ABM method is that the times of embedding 0 (1) should not exceed the amounts of elements originally in the left (right) bins, respectively. During the embedding process, we need to count the numbers of elements mapped to both bins, respectively. Once the time of embedding 0 (or 1) has caught up with the amount of elements originally in the left (or right) bin, no bit value can be further embedded to ensure the bijective mapping between the elements in the original object and those in the stego object.
falls into the left bin, it represents a bit value of 0, otherwise 1 if it is in the right bin. To embed a bit value of 0, an element should be kept in the left bin if it was originally the case, or moved to the left bin if it originally was in the right one. The process to embed a bit value of 1 is similar as long as we replace "left" by "right" and vice versa. The key idea of the ABM method is that the times of embedding 0 (1) should not exceed the amounts of elements originally in the left (right) bins, respectively. During the embedding process, we need to count the numbers of elements mapped to both bins, respectively. Once the time of embedding 0 (or 1) has caught up with the amount of elements originally in the left (or right) bin, no bit value can be further embedded to ensure the bijective mapping between the elements in the original object and those in the stego object.
An illustration of the embedding process is shown in Figure 2, where eleven elements  with different values are in the Unit
with different values are in the Unit  . Suppose the elements are processed in their index order to embed a string of bit values "10011010010". Since
. Suppose the elements are processed in their index order to embed a string of bit values "10011010010". Since  is in the left bin, it corresponds to the bit value 0. Therefore, it should be moved to the right bin to embed a bit value 1. For
is in the left bin, it corresponds to the bit value 0. Therefore, it should be moved to the right bin to embed a bit value 1. For  , it should remain in the left bin to embed a bit value 0. To embed the third bit value 0 in the string,
, it should remain in the left bin to embed a bit value 0. To embed the third bit value 0 in the string,  needs to be moved from the right to the left bin. The rest of bit values are sequentially embedded until the ninth one, which leads
needs to be moved from the right to the left bin. The rest of bit values are sequentially embedded until the ninth one, which leads  to remain in the left bin. Since the number of elements mapped to the left bin of stego object has reached 5, which is the amount of elements in the original object, no bit value can be embedded in the Unit
to remain in the left bin. Since the number of elements mapped to the left bin of stego object has reached 5, which is the amount of elements in the original object, no bit value can be embedded in the Unit  any more. Therefore, only the first nine bit values "100110100" can be embedded by mapping the elements with the indices 2, 3, 6, 8, and 9 into the left bin and the remaining elements into the right bin to generate the stego object. To minimize the distortion of cover object in the mean square error (MSE) criterion, the elements in the same bin should be ordered according to their original values. In the optimal scheme,
any more. Therefore, only the first nine bit values "100110100" can be embedded by mapping the elements with the indices 2, 3, 6, 8, and 9 into the left bin and the remaining elements into the right bin to generate the stego object. To minimize the distortion of cover object in the mean square error (MSE) criterion, the elements in the same bin should be ordered according to their original values. In the optimal scheme,  will have the values of
will have the values of  , while the values of
, while the values of  are modified to those of
are modified to those of  to generate the stego object.
to generate the stego object.
If all the elements originally in the same bin have the identical values, there is no need to sort the elements mapped to that bin. Otherwise, the mapping process minimizing the distortion depends on the order the elements are processed. In Figure 3, the same elements as shown in Figure 2 are used to embed the bit values "100110100" except that the indices of the ninth and tenth ones are exchanged. To embed the ninth bit value 0, the element  should be moved from the right bin to the left one, while it remains in the left bin in Figure 2. To minimize the distortion in the MSE criterion, the elements
should be moved from the right bin to the left one, while it remains in the left bin in Figure 2. To minimize the distortion in the MSE criterion, the elements  will have the values of
will have the values of  , while the values of
, while the values of  are changed to those of
are changed to those of  , respectively.
, respectively.
The decoding process is much simpler: given the same scanning order as in the embedding process, the bit values can be extracted from the element positions (i.e., in the left or right bin) one by one. The extracted bit value will be 0 if an element is located in the left bin, or 1 if it is in the right one. For each embedding unit, once all elements in one bin (left or right) have been used up, the extraction process is finished. For example, the bit values that can be extracted from the Unit  in Figures 2(b) and 3(b) are not "10011010011" but "100110100". Since the embedding and extraction operations in one unit do not interfere with those performed in other units, the operations in every embedding unit can be carried out in parallel. So both encoding and decoding processes can be performed according to the scrambled indices of all elements with a secret key shared by the sender and receiver.
in Figures 2(b) and 3(b) are not "10011010011" but "100110100". Since the embedding and extraction operations in one unit do not interfere with those performed in other units, the operations in every embedding unit can be carried out in parallel. So both encoding and decoding processes can be performed according to the scrambled indices of all elements with a secret key shared by the sender and receiver.
The hiding rate is maximized if the maximum number of 0s or 1s are embedded. A parameter  can be used to adjust the hiding rate, that is, the embedding process stops once the number of embedded bits reaches a fraction of the amount originally in one bin (left or right). Accordingly, the same value of
can be used to adjust the hiding rate, that is, the embedding process stops once the number of embedded bits reaches a fraction of the amount originally in one bin (left or right). Accordingly, the same value of  should be used in the extraction process. Suppose there are
should be used in the extraction process. Suppose there are  and
and  elements in the two bins of an embedding unit. Without loss of generality, we assume that
elements in the two bins of an embedding unit. Without loss of generality, we assume that  is always inferior to
is always inferior to  , then the minimum and maximum amount of bits that can be embedded are
, then the minimum and maximum amount of bits that can be embedded are  and
and  . With the parameter
. With the parameter  , the low and upper bounds of capacity in that unit will be
, the low and upper bounds of capacity in that unit will be  and
and  bits, where
bits, where  represents the ceil function. So the hiding rate can be adjusted with the parameter
represents the ceil function. So the hiding rate can be adjusted with the parameter  , which should be shared by the sender and receiver.
, which should be shared by the sender and receiver.
2.2. Steganography in 3D Geometries Using the ABM Method
In literature, a majority of steganography research has been conducted on digital images for their popularity. With the development of 3D scanning and modeling techniques, more and more 3D models have been used for geometry representation. With the dissemination such as using the virtual reality modeling language (VRML) [31] to represent 3D graphics on the Web, 3D models have become potential covers for covert communication. In the following, the ABM method is applied to 3D geometry with coordinates.
Suppose there are  vectors of position in a 3D geometry represented by
vectors of position in a 3D geometry represented by  , where a vector
, where a vector  specifies the coordinates
specifies the coordinates  in
in  for
for  . The proposed mapping method can be applied to three coordinates sets
. The proposed mapping method can be applied to three coordinates sets  ,
,  , and
, and  on the
on the  ,
,  , and
, and  axes with the same bin size
axes with the same bin size  , respectively. Firstly, the histogram of coordinates on each axis, that is, the number of coordinates in every bin, needs to be calculated. For the cover object represented by floating point number, the computation of histograms can be subject to the smallest value within it. For instance, by denoting the smallest value among the coordinates on the
, respectively. Firstly, the histogram of coordinates on each axis, that is, the number of coordinates in every bin, needs to be calculated. For the cover object represented by floating point number, the computation of histograms can be subject to the smallest value within it. For instance, by denoting the smallest value among the coordinates on the  axis as
axis as  , we calculate the value of
, we calculate the value of  . For each value
. For each value  in a 3D geometry, we know it is located in the
in a 3D geometry, we know it is located in the  th bin from the starting point
th bin from the starting point  . Since the embedding process does not generate new values, the value of
. Since the embedding process does not generate new values, the value of  can also be obtained from the smallest coordinate in the stego geometry with the value of
can also be obtained from the smallest coordinate in the stego geometry with the value of  . Therefore, the histograms of stego geometry, which are the same as the original ones, can be calculated to extract the embedded data. Figure 4 shows the original and stego geometries "gears" using the ABM method. The distortion of stego geometry is measured with the 3D signal-to-noise ratio (SNR) defined in [32]. By setting the value of Δ at 0.005 and the parameter
. Therefore, the histograms of stego geometry, which are the same as the original ones, can be calculated to extract the embedded data. Figure 4 shows the original and stego geometries "gears" using the ABM method. The distortion of stego geometry is measured with the 3D signal-to-noise ratio (SNR) defined in [32]. By setting the value of Δ at 0.005 and the parameter  , the 3D SNR of the stego geometry "gears" is 63.8260 (dB). As the embedding process does not generate new values, the marginal distribution of cover geometry is preserved.
, the 3D SNR of the stego geometry "gears" is 63.8260 (dB). As the embedding process does not generate new values, the marginal distribution of cover geometry is preserved.
3. Image Steganography with the 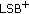 Algorithm
Algorithm
To apply the ABM method to digital images, in which the pixel values are represented by integers, the bin size  is set at 1 to minimize the distortion. As shown in Figure 5, every two adjacent pixel values within
is set at 1 to minimize the distortion. As shown in Figure 5, every two adjacent pixel values within  are used to form an embedding unit, respectively. The bit value corresponding to each bin has not been labeled because it can be directly extracted from the LSB of pixel value. Since the mapping is always performed in the same unit, only the LSB of pixel value is changeable. So the ABM method becomes a kind of LSB hiding, namely, the
are used to form an embedding unit, respectively. The bit value corresponding to each bin has not been labeled because it can be directly extracted from the LSB of pixel value. Since the mapping is always performed in the same unit, only the LSB of pixel value is changeable. So the ABM method becomes a kind of LSB hiding, namely, the  algorithm.
algorithm.
3.1. The  Algorithm
Algorithm
Given a gray-scale image, its histogram is calculated by counting the pixels with the same value, that is, the amount of pixels within every bin. Since the operations in one embedding unit are independent from those in the other units, we only discuss the operations in an arbitrary unit. In the normal LSB hiding, a string of bit values are used to replace the LSBs of pixel values. The histogram of cover image is probably changed due to the randomness of embedded data. Obviously, the histogram will be preserved if the amount of pixels within each bin is unchanged. So we constrain the replacement operations in the  algorithm. As discussed previously in the general method, the key idea is that the number of embedded 0s and 1s should not exceed the original ones in the LSBs. Suppose that there are
algorithm. As discussed previously in the general method, the key idea is that the number of embedded 0s and 1s should not exceed the original ones in the LSBs. Suppose that there are  and
and  pixels originally in the left and right bins of a unit, the time of embedding 0 should be no more than
pixels originally in the left and right bins of a unit, the time of embedding 0 should be no more than  , and the time of embedding 1 should not exceed
, and the time of embedding 1 should not exceed  , respectively. Once there are
, respectively. Once there are  0s (or
0s (or  1s) having been embedded, all the rest LSBs should be replaced with 1s (or 0s). In this way, the amounts of 0s and 1s in the LSBs are unchanged by data embedding. In the decoding process, the embedded bits are extracted one by one in the same order as in the embedding process. The extraction process is finished as soon as all LSBs in one bin (either left or right) have been extracted. Since part of the LSBs are used to repair the cover histogram, a portion of capacity is sacrificed.
1s) having been embedded, all the rest LSBs should be replaced with 1s (or 0s). In this way, the amounts of 0s and 1s in the LSBs are unchanged by data embedding. In the decoding process, the embedded bits are extracted one by one in the same order as in the embedding process. The extraction process is finished as soon as all LSBs in one bin (either left or right) have been extracted. Since part of the LSBs are used to repair the cover histogram, a portion of capacity is sacrificed.
3.2. The Histogram Tail Detection
For an embedding unit of pixel values, we define the metric of histogram tail as the number of pixels that has not been scanned in one bin until all pixels in the other bin have been. Given the Unit  as shown in Figure 6, there are two pixels in the left bin after the
as shown in Figure 6, there are two pixels in the left bin after the  pixels in the right bin have been scanned in a certain order. Then the histogram tail for Unit
pixels in the right bin have been scanned in a certain order. Then the histogram tail for Unit  is 2 in that scanning order. Obviously, the definition of histogram tail depends on the order in which the pixels are scanned. If we intentionally scan the pixels with value
is 2 in that scanning order. Obviously, the definition of histogram tail depends on the order in which the pixels are scanned. If we intentionally scan the pixels with value  before all those with value
before all those with value  , the histogram tail will be
, the histogram tail will be  . By employing the same scanning order as in the embedding process, the histogram tail is actually the number of pixels used to repair the histogram. Take the Unit
. By employing the same scanning order as in the embedding process, the histogram tail is actually the number of pixels used to repair the histogram. Take the Unit  in Figure 6, for instance, after
in Figure 6, for instance, after  1s have been embedded by mapping
1s have been embedded by mapping  pixels to the right bin of stego object, the last 2 pixels must be mapped to the left bin to preserve the histogram.
pixels to the right bin of stego object, the last 2 pixels must be mapped to the left bin to preserve the histogram.
The  hiding significantly affects the histogram tail of cover image. If the hiding is performed in the raster order, that is, by rows from top to bottom and within each row from left to right, the histogram tail of the 128 units (from
hiding significantly affects the histogram tail of cover image. If the hiding is performed in the raster order, that is, by rows from top to bottom and within each row from left to right, the histogram tail of the 128 units (from  to
to  ) is greatly increased by implementing the
) is greatly increased by implementing the  algorithm with
algorithm with  , as shown in Figure 7. This phenomenon is caused because the two bins in the same unit contain different numbers of pixels, while a secret message consists of almost the same number of 0s and 1s. Due to the interdependencies between the neighboring pixels, the pixels within the same unit are closely distributed in a natural image. That means we can probably find a pixel nearby another one with the same binary value except in the LSB. Therefore, the histogram tail of an original image in the raster order is generally small. When the
, as shown in Figure 7. This phenomenon is caused because the two bins in the same unit contain different numbers of pixels, while a secret message consists of almost the same number of 0s and 1s. Due to the interdependencies between the neighboring pixels, the pixels within the same unit are closely distributed in a natural image. That means we can probably find a pixel nearby another one with the same binary value except in the LSB. Therefore, the histogram tail of an original image in the raster order is generally small. When the  hiding is performed in the raster order to embed a secret message with the equal number of 0s and 1s, the bin with less pixels will normally be firstly filled so that the rest pixels are all in the other bin. Therefore, the histogram tail of stego image in the same order is significantly increased.
hiding is performed in the raster order to embed a secret message with the equal number of 0s and 1s, the bin with less pixels will normally be firstly filled so that the rest pixels are all in the other bin. Therefore, the histogram tail of stego image in the same order is significantly increased.
To avoid the histogram tail detection, one way is to perform the  hiding in a pseudorandom order by permuting the pixel indices with a secret key. Without the key, a steganalyst does not know the correct order employed in the embedding process. As we have discussed, the histogram tail for each unit depends on the order in which the pixels are processed. It will be suspicious to have a large histogram tail in the raster order but a large histogram tail in a special order does not carry much information as it happens in a natural image. After we perform the
hiding in a pseudorandom order by permuting the pixel indices with a secret key. Without the key, a steganalyst does not know the correct order employed in the embedding process. As we have discussed, the histogram tail for each unit depends on the order in which the pixels are processed. It will be suspicious to have a large histogram tail in the raster order but a large histogram tail in a special order does not carry much information as it happens in a natural image. After we perform the  hiding with
hiding with  in a random order, the histogram tail of stego image in the raster order is close to that of original image, as shown in Figure 8.
in a random order, the histogram tail of stego image in the raster order is close to that of original image, as shown in Figure 8.
3.3. Preventing the Steganalytic Algorithms Based on HCF
The histogram characteristic function (HCF), defined as the discrete Fourier transform (DFT) of image histogram, is first used by Harmsen and Pearlman [10] for the detection of additive noise steganography. Based on HCF, the center of mass (COM) is calculated by

where  is the HCF,
is the HCF,  , and
, and  is the DFT length. For gray-scale images,
is the DFT length. For gray-scale images,  . Since the
. Since the  algorithm does not change the cover histogram, the HCF and COM of cover image are both preserved. Therefore, the steganalytic algorithms that are simply based on the COM of HCF (HCF-COM) are prevented.
algorithm does not change the cover histogram, the HCF and COM of cover image are both preserved. Therefore, the steganalytic algorithms that are simply based on the COM of HCF (HCF-COM) are prevented.
In [11], two ways of applying the HCF are further proposed to detect the LSB matching steganography in the gray-scale images. The first algorithm downsamples a suspected image by a factor of two in both dimensions using an averaging filter. Then the downsampled image is used to calibrate the HCF-COM of the full-sized image. It is observed that for the presence of LSB matching steganography, the HCF-COM of the full-sized image is more affected than the one of the downsampled image. As for an image without the hidden data, HCF-COMs of the downsampled and full-sized images are roughly the same. In the second algorithm, the two-dimensional adjacency histogram is used instead of the standard one for steganalysis by considering one horizontal neighboring pixel. Since the adjacent pixels tend to have close intensities, the adjacency histogram is sparse off the diagonal.
Although the cover histogram is unchanged by the  algorithm, the histogram of the downsampled image is not preserved for it is a high-order metric. As we can see from Figure 9, noticeable change has been made to the histogram of the downsampled image after performing the
algorithm, the histogram of the downsampled image is not preserved for it is a high-order metric. As we can see from Figure 9, noticeable change has been made to the histogram of the downsampled image after performing the  algorithm on the image "Oregon" with
algorithm on the image "Oregon" with  . So the
. So the  algorithm would probably be detected by the steganalytic algorithms in [11] if applied on all pixels of a cover image. To improve the security, we need to preserve the histogram of the downsampled image first. If we perform the
algorithm would probably be detected by the steganalytic algorithms in [11] if applied on all pixels of a cover image. To improve the security, we need to preserve the histogram of the downsampled image first. If we perform the  hiding on the subsets of pixels with the same right, up, and up-right neighbor values (see in Figure 10 for the selection of those pixels), only one out of the four pixels in a downsampling unit may be changed for data embedding or compensation. As the histogram of pixels in the same subset is preserved by the
hiding on the subsets of pixels with the same right, up, and up-right neighbor values (see in Figure 10 for the selection of those pixels), only one out of the four pixels in a downsampling unit may be changed for data embedding or compensation. As the histogram of pixels in the same subset is preserved by the  algorithm, the histogram of downsampled values is also unchanged.
algorithm, the histogram of downsampled values is also unchanged.
The pixels in black are chosen as the neighbors of others so that only the light-colored pixels with the same five neighbor values (left, right, up, down, and up-right) are grouped into a subset. As for the light-colored pixels in the leftmost column, only the right, up, down, and up-right neighbor values are considered, while the left, right, up, and up-right neighbor values are taken into account for the light-colored pixels in the bottom row.
To preserve the adjacency histogram as suggested in [11], the left and right neighbor values of every pixel in a selected subset should be the same. If the two-dimensional adjacency histogram is calculated vertically, the pixel values up and down the current one should also be the same. So we perform the  hiding on the subsets of pixels having the same five neighbor values (left, right, up, down, and up-right, denoted by 5-N in short) as shown in Figure 10, where the pixels marked in black are chosen as the neighbors of others, that is, only the light-colored pixels are grouped into a subset if they have the same five neighbor values. As for the light-colored pixels in the leftmost column and in the bottom row, only four neighbor values are considered so that they are separately treated, respectively.
hiding on the subsets of pixels having the same five neighbor values (left, right, up, down, and up-right, denoted by 5-N in short) as shown in Figure 10, where the pixels marked in black are chosen as the neighbors of others, that is, only the light-colored pixels are grouped into a subset if they have the same five neighbor values. As for the light-colored pixels in the leftmost column and in the bottom row, only four neighbor values are considered so that they are separately treated, respectively.
By implementing the  algorithm in the 5-N way, the histograms of cover image and its downsampled version, the adjacency histogram of cover image, are all preserved. As a result, HCF-COMs of the full-sized and downsampled images, the two-dimensional COM based on the adjacency histogram, are unchanged by the hidden data. So the steganalytic algorithms in [11] to detect the LSB matching steganography and the SPA steganalysis in [9] to detect the random LSB hiding are prevented in principle. Moreover, all the steganalytic algorithms using the first-order statistics of cover image are not efficient because the marginal distribution is inherently preserved by the
algorithm in the 5-N way, the histograms of cover image and its downsampled version, the adjacency histogram of cover image, are all preserved. As a result, HCF-COMs of the full-sized and downsampled images, the two-dimensional COM based on the adjacency histogram, are unchanged by the hidden data. So the steganalytic algorithms in [11] to detect the LSB matching steganography and the SPA steganalysis in [9] to detect the random LSB hiding are prevented in principle. Moreover, all the steganalytic algorithms using the first-order statistics of cover image are not efficient because the marginal distribution is inherently preserved by the  algorithm.
algorithm.
4. Experimental Results
4.1. Steganography in 3D Geometries
The proposed ABM method was implemented on the 3D VRML models listed in Table 1 (downloaded from http://www.martinreddy.net/ukvrsig/vrml.html), in which the coordinates are represented by floating point numbers. The 3D signal-to-noise ratio (3D SNR) as defined in [32] is used to represent the distortion of stego geometry. As the modification of each coordinate in the cover geometry is bounded by  2
2 , we required that the 3D SNR of stego geometry to be greater than 60 (dB) by adjusting the bin size
, we required that the 3D SNR of stego geometry to be greater than 60 (dB) by adjusting the bin size  , as shown in Table 1.
, as shown in Table 1.
A trade-off between the distortion and the data hiding rate exists for 3D geometry. As shown in Figure 11, the data hiding rate is low when the bin size is tiny because there are few coordinates in the same bin. When there is no coordinate in one bin, no data can be embedded despite how many coordinates in the other bin of the same embedding unit are present. If the value of  is increased within a certain range, the coordinates are more equally distributed in each bin of an embedding unit so that the data hiding rate is increased. Meanwhile, more geometrical distortion is caused when the bin size is increased. If the bin size is adaptively chosen to make the distortion unnoticeable, it should be sent to the receiver for decoding.
is increased within a certain range, the coordinates are more equally distributed in each bin of an embedding unit so that the data hiding rate is increased. Meanwhile, more geometrical distortion is caused when the bin size is increased. If the bin size is adaptively chosen to make the distortion unnoticeable, it should be sent to the receiver for decoding.
With the ABM method, steganography in the cover object represented by floating point numbers is enabled, such as 3D geometrical models with coordinates. Since the previous steganalysis archives are mainly dedicated to images, techniques to detect the hidden data in the other multimedia content are still rare. A secret key shared by the sender and receiver can be used to scramble the element indices to perform the hiding in a pseudorandom order. Since the bin size can be adaptively chosen for the cover object represented by the floating point numbers, it can also be used as a secret key to decode the hidden message from the stego object.
4.2. Steganography in Images
The  algorithm was implemented with
algorithm was implemented with  on 1000 gray images provided by BOWS-2 [33] in the 5-N way, that is, on every subset of pixels having the same five neighbor values (left, right, up, down, and up-right). It should be noted that the original unmarked images from BOWS2 have been JPEG compressed, scaled, and cropped to the final format and were recommended to be used for experimental evaluation in this special issue. Table 2 lists a few images used in the experiments and the number of bits that can be embedded, respectively. The peak signal-to-noise ratio (PSNR) of the stego images was calculated by setting the maximum pixel value to 255.
on 1000 gray images provided by BOWS-2 [33] in the 5-N way, that is, on every subset of pixels having the same five neighbor values (left, right, up, down, and up-right). It should be noted that the original unmarked images from BOWS2 have been JPEG compressed, scaled, and cropped to the final format and were recommended to be used for experimental evaluation in this special issue. Table 2 lists a few images used in the experiments and the number of bits that can be embedded, respectively. The peak signal-to-noise ratio (PSNR) of the stego images was calculated by setting the maximum pixel value to 255.
As shown in Table 2, the PSNRs of the stego images are all above 60 (dB) when the  algorithm is implemented in the 5-N way with
algorithm is implemented in the 5-N way with  . Not surprisingly, the PSNR is higher when less bits are hidden in a stego image. From the experimental results, it can be seen that the capacity varies from one image to another. For a cover image consisting of many pixels having the same neighbor values, the hiding rate is high. Otherwise, for a cover image such as "Fall" in which this is hardly the case, only a few bits can be embedded. As shown in Figure 10, only one out of four pixel values is possible to be modified if the
. Not surprisingly, the PSNR is higher when less bits are hidden in a stego image. From the experimental results, it can be seen that the capacity varies from one image to another. For a cover image consisting of many pixels having the same neighbor values, the hiding rate is high. Otherwise, for a cover image such as "Fall" in which this is hardly the case, only a few bits can be embedded. As shown in Figure 10, only one out of four pixel values is possible to be modified if the  algorithm is implemented in the 5-N way. In our experiments, the hiding rate is normally no more than 0.06 bit/pixel. Compared with applying the
algorithm is implemented in the 5-N way. In our experiments, the hiding rate is normally no more than 0.06 bit/pixel. Compared with applying the  algorithm in the 4-N way (left, right, up, and down) [30], the capacity in the 5-N way is lower because the requirement on the neighbor values of pixels within a selected subset is stricter, as shown in Table 2.
algorithm in the 4-N way (left, right, up, and down) [30], the capacity in the 5-N way is lower because the requirement on the neighbor values of pixels within a selected subset is stricter, as shown in Table 2.
The experimental results show that the histogram of downsampled image is well preserved, that is, there is no difference between the histograms of two images downsampled from the original and stego ones, respectively. We use  and
and  to denote the HCF-COMs of original image and its downsampled version, while
to denote the HCF-COMs of original image and its downsampled version, while  and
and  are used to denote the HCF-COMs of stego image and its downsampled version. The HCF-COMs of 1000 stego images and their downsampled versions are shown in Figure 12, which are exactly the same as those of original images.
are used to denote the HCF-COMs of stego image and its downsampled version. The HCF-COMs of 1000 stego images and their downsampled versions are shown in Figure 12, which are exactly the same as those of original images.
As pointed out in [11], the value of  is close to that of
is close to that of  . By performing the
. By performing the  hiding in the 5-N way, the values of
hiding in the 5-N way, the values of  and
and  are identical to those of
are identical to those of  and
and  so that
so that  . As shown in Figure 13 for the first 1000 gray images in BOWS-2, the difference between HCF-COM of the downsampled and full-sized images, that is,
. As shown in Figure 13 for the first 1000 gray images in BOWS-2, the difference between HCF-COM of the downsampled and full-sized images, that is,  , is the same for the original image and the stego image generated by the
, is the same for the original image and the stego image generated by the  algorithm in the 5-N way. Therefore, the difference between the two HCF-COMs (i.e., of the full-sized and downsampled images) cannot be used to distinguish the stego images from the clean ones in the case that the
algorithm in the 5-N way. Therefore, the difference between the two HCF-COMs (i.e., of the full-sized and downsampled images) cannot be used to distinguish the stego images from the clean ones in the case that the  algorithm is applied in the 5-N way. It should be noted that this conclusion does not depend on the data used here, and the same results can be obtained from other image sets.
algorithm is applied in the 5-N way. It should be noted that this conclusion does not depend on the data used here, and the same results can be obtained from other image sets.
Meanwhile, the adjacency histogram was also preserved by applying the  algorithm in the 5-N way, so that the steganalytic algorithms in [11] and the SPA steganalysis in [9] are both prevented. Furthermore, histogram tail of the cover image in the raster order was rarely changed. For the six images listed in Table 2, the experimental results show that the histogram tail in the raster order was unchanged by the hidden message. However, it is not yet possible to claim that the proposed algorithm is practically secure before other steganalysis algorithms using the high-order statistics would have been tested. Recently, high-order statistical features have been used by supervised learning for steganalysis; our future work includes to investigate if the proposed algorithm can resist those blind learning-based algorithms (e.g., [16]).
algorithm in the 5-N way, so that the steganalytic algorithms in [11] and the SPA steganalysis in [9] are both prevented. Furthermore, histogram tail of the cover image in the raster order was rarely changed. For the six images listed in Table 2, the experimental results show that the histogram tail in the raster order was unchanged by the hidden message. However, it is not yet possible to claim that the proposed algorithm is practically secure before other steganalysis algorithms using the high-order statistics would have been tested. Recently, high-order statistical features have been used by supervised learning for steganalysis; our future work includes to investigate if the proposed algorithm can resist those blind learning-based algorithms (e.g., [16]).
5. Conclusion
In this paper, we have presented the adjacent bin mapping (ABM) method for steganography and applied it to 3D geometrical models. By choosing an appropriate bin size, little distortion has been introduced to the VRML models to hide a secret message. Therefore, how to detect the secret message hidden in 3D geometries should be further investigated as well as in other covers represented by floating point numbers.
When applied to the gray-scale images, the ABM method becomes a kind of LSB hiding, namely, the  algorithm. The histogram tail has been defined to detect the
algorithm. The histogram tail has been defined to detect the  hiding in the raster order, and we have avoided the detection by performing the hiding in a pseudorandom order. To prevent the steganalytic algorithms in [11] to detect the LSB matching steganography, the pixels with the same five neighbor values (i.e., left, right, up, down, and up-right) have been grouped into each subset. It has been shown that several high-order statistics are preserved by applying the
hiding in the raster order, and we have avoided the detection by performing the hiding in a pseudorandom order. To prevent the steganalytic algorithms in [11] to detect the LSB matching steganography, the pixels with the same five neighbor values (i.e., left, right, up, down, and up-right) have been grouped into each subset. It has been shown that several high-order statistics are preserved by applying the  algorithm on the selected subsets of pixels. Our future work is to investigate if the proposed algorithm also resists to the blind learning-based steganalysis (e.g., [16]).
algorithm on the selected subsets of pixels. Our future work is to investigate if the proposed algorithm also resists to the blind learning-based steganalysis (e.g., [16]).
References
Anderson RJ, Petitcolas FAP: On the limits of steganography. IEEE Journal on Selected Areas in Communications 1998, 16(4):474-481. 10.1109/49.668971
Petitcolas FAP, Anderson RJ, Kuhn MG: Information hiding—a survey. Proceedings of the IEEE 1999, 87(7):1062-1078. 10.1109/5.771065
Simmons GJ: The prisoner's problem and the subliminal channel. In Advances in Cryptology, Lecture Notes in Computer Science. Volume 196. Plenum Press, New York, NY, USA; 1994:51-67.
Cachin C: An information theoretic model for steganography. Proceedings of the 2nd International Workshop on Information Hiding (IH '98), April 1998, Portland, Ore, USA, Lecture Notes in Computer Science 1525: 306-318.
Johnson NF, Jajodia S: Steganalysis of images created using current steganography software. Proceedings of the 2nd International Workshop on Information Hiding (IH '98), April 1998, Portland, Ore, USA, Lecture Notes in Computer Science 1525: 273-289.
Westfeld A, Pfitzmann A: Attacks on steganographic systems. Proceedings of the 3rd International Workshop on Information Hiding (IH '99), September-October 1999, Dresden, Germany, Lecture Notes in Computer Science 1768: 61-76.
Provos N, Honeyman P: Detecting steganographic content on the internet. Proceedings of the ISOC Network and Distributed System Security Symposium (NDSS '02), February 2002, San Diego, Calif, USA 2-13.
Fridrich J, Goljan M, Du R: Reliable detection of LSB steganography in color and grayscale images. Proceedings of the ACM Workshop on Multimedia and Security, October 2001, Ottawa, Canada 27-30.
Dumitrescu S, Wu X, Wang Z: Detection of LSB steganography via sample pair analysis. IEEE Transactions on Signal Processing 2003, 51(7):1995-2007. 10.1109/TSP.2003.812753
Harmsen JJ, Pearlman WA: Steganalysis of additive noise modelable information hiding. Security and Watermarking of Multimedia Contents V, January 2003, Santa Clara, Calif, USA, Proceedings of SPIE 5020: 131-142.
Ker AD: Steganalysis of LSB matching in grayscale images. IEEE Signal Processing Letters 2005, 12(6):441-444. 10.1109/LSP.2005.847889
Wang Y, Moulin P: Steganalysis of block-structured stegotext. Security, Steganography, and Watermaking of Multimedia Contents VI, January 2004, San Jose, Calif, USA, Proceedings of SPIE 5306: 477-488.
Sullivan K, Madhow U, Chandrasekaran S, Manjunath BS: Steganalysis for Markov cover data with applications to images. IEEE Transactions on Information Forensics and Security 2006, 1(2):275-287. 10.1109/TIFS.2006.873595
Avcibaş I, Memon N, Sankur B: Steganalysis using image quality metrics. IEEE Transactions on Image Processing 2003, 12(2):221-229. 10.1109/TIP.2002.807363
Lyu S, Farid H: Steganalysis using color wavelet statistics and one-class support vector machines. Security, Steganography, and Watermaking of Multimedia Contents VI, January 2004, San Jose, Calif, USA, Proceedings of SPIE 5306: 35-45.
Lyu S, Farid H: Steganalysis using higher-order image statistics. IEEE Transactions on Information Forensics and Security 2006, 1(1):111-119. 10.1109/TIFS.2005.863485
Wang Y, Moulin P: Optimized feature extraction for learning-based image steganalysis. IEEE Transactions on Information Forensics and Security 2007, 2(1):31-45. 10.1109/TIFS.2006.890517
Fridrich J, Goljan M, Hogea D: Steganalysis of JPEG images: breaking the F5 algorithm. Proceedings of the 5th International Workshop on Information Hiding (IH '02), October 2002, Noordwijkerhout, The Netherlands, Lecture Notes in Computer Science 2578: 310-323.
Fridrich J, Goljan M, Hogea D: Attacking the outguess. Proceedings of the ACM Workshop on Multimedia and Security, December 2002, Juan-Pins, France 967-982.
Böhme R, Westfeld A: Exploiting preserved statistics for steganalysis. Proceedings of the 6th International Workshop on Information Hiding (IH '04), May 2004, Toronto, Canada, Lecture Notes in Computer Science 3200: 82-96.
Böhme R, Westfeld A: Breaking cauchy model-based JPEG steganography with first order statistics. In Proceedings of 9th European Symposium on Research in Computer Security (ESORICS '04), September 2004, Sophia Antipolis, France, Lecture Notes in Computer Science Edited by: Samarati P, Ryan PYA, Gollmann D, Molva R. 3193: 125-140.
Westfeld A: F5—a steganographic algorithm: high capacity despite better steganalysis. Proceedings of the 4th International Workshop on Information Hiding (IH '01), April 2001, Pittsburgh, Pa, USA, Lecture Notes in Computer Science 2137: 289-302.
Provos N: Defending against statistical steganalysis. Proceedings of the 10th Conference on USENIX Security Symposium, August 2001, Washington DC, USA 323-335.
Franz E: Steganography preserving statistical properties. Proceedings of the 5th International Workshop on Information Hiding (IH '02), October 2002, Noordwijkerhout, The Netherlands, Lecture Notes in Computer Science 2578: 278-294.
Eggers JJ, Bäuml R, Girod B: A communications approach to image steganography. Security and Watermarking of Multimedia Contents IV, January 2002, San Jose, Calif, USA, Proceedings of SPIE 4675: 26-37.
Tzschoppe R, Bäuml R, Huber JB, Kaup A: Steganographic system based on higher-order statistics. Security and Watermarking of Multimedia Contents V, January 2003, Santa Clara, Calif, USA, Proceedings of SPIE 5020: 156-166.
Solanki K, Sullivan K, Madhow U, Manjunath BS, Chandrasekaran S: Provably secure steganography: achieving zero K-L divergence using statistical restoration. Proceedings of IEEE International Conference on Image Processing (ICIP '06), Octobor 2006, Atlanta, Ga, USA 125-128.
Sarkar A, Solanki K, Madhow U, Chandrasekaran S, Manjunath BS: Secure steganography: statistical restoration of the second order dependencies for improved security. Proceedings of the 32nd IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '07), April 2007, Honolulu, Hawaii, USA 2: 277-280.
Sallee P: Model-based steganography. Proceedings of the 2nd International Workshop on Digital Watermarking (IWDW '03), October 2003, Seoul, Korea, Lecture Notes in Computer Science 2939: 154-167.
Wu H-T, Dugelay J-L, Cheung Y-M: A data mapping method for steganography and its application to images. Proceedings of the 10th International Workshop on Information Hiding (IH '08), May 2008, Santa Barbara, Calif, USA, Lecture Notes in Computer Science 5284: 236-250.
ISO/IEC DIS 14772-1 : The virtual reality modeling language. http://www.web3d.org/x3d/specifications/vrml
Wu H-T, Dugelay J-L: Reversible watermarking of 3D mesh models by prediction-error expansion. Proceedings of the 10th IEEE International Workshop on Multimedia Signal Processing (MMSP '08), October 2008, Cairns, Australia 797-802.
Break our watermarking system 2nd Ed http://bows2.gipsa-lab.inpg.fr/
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wu, HT., Dugelay, JL. Steganography in 3D Geometries and Images by Adjacent Bin Mapping. EURASIP J. on Info. Security 2009, 317165 (2009). https://doi.org/10.1155/2009/317165
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/317165


 in the embedding Unit n are used to embed a string of bit values "10011010010". Only the first nine bit values "100110100" can be embedded by mapping the eleven elements to generate the stego object on the right with the minimum mean square error (MSE).
in the embedding Unit n are used to embed a string of bit values "10011010010". Only the first nine bit values "100110100" can be embedded by mapping the eleven elements to generate the stego object on the right with the minimum mean square error (MSE).

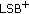 Algorithm
Algorithm
 Algorithm
Algorithm






 and (Y-axis)
and (Y-axis)  for the first 1000 gray images provided by BOWS-2.
for the first 1000 gray images provided by BOWS-2.
 of the original image is the same as (Y-axis)
of the original image is the same as (Y-axis)  of the stego image generated in the 5-N way for the first 1000 gray images in BOWS-2.
of the stego image generated in the 5-N way for the first 1000 gray images in BOWS-2.