- Research Article
- Open access
- Published:
How Reed-Solomon Codes Can Improve Steganographic Schemes
EURASIP Journal on Information Security volume 2009, Article number: 274845 (2009)
Abstract
The use of syndrome coding in steganographic schemes tends to reduce distortion during embedding. The more complete model comes from the wet papers (J. Fridrich et al., 2005) and allow to lock positions which cannot be modified. Recently, binary BCH codes have been investigated and seem to be good candidates in this context (D. Schönfeld and A. Winkler, 2006). Here, we show that Reed-Solomon codes are twice better with respect to the number of locked positions; in fact, they are optimal. First, a simple and efficient scheme based on Lagrange interpolation is provided to achieve the optimal number of locked positions. We also consider a new and more general problem, mixing wet papers (locked positions) and simple syndrome coding (low number of changes) in order to face not only passive but also active wardens. Using list decoding techniques, we propose an efficient algorithm that enables an adaptive tradeoff between the number of locked positions and the number of changes.
1. Introduction
Steganography aims at sending a message through a cover-medium, in an undetectable way. Undetectable means that nobody, except the intended receiver of the message, should be able to tell if the medium is carrying a message or not [1]. Hence, if we speak about still images as cover-media, the embedding should work with the smallest possible distortion, not being detectable with the quite powerful analysis tools available [2, 3]. A lot of papers have been published on this topic, and it appears that modeling the embedding and detection/extraction processes with an error correcting code point of view, usually called matrix embedding by the steganographic community, may be helpful to achieve these goals [4–15]. The main interest of this approach is that it decreases the number of components modifications during the embedding process. As a side effect, it was remarked in [8] that matrix embedding could be used to provide an effective answer to the adaptive selection channel problem. The sender can embed the messages adaptively with the cover-medium to minimize the distortion, and the receiver can extract the messages without being aware of the sender choices. A typical steganographic application is the perturbed quantization [16]; during quantization process, for example, JPEG compression, real values  have to be rounded between possible quantized values
have to be rounded between possible quantized values  ; when
; when  lies close to the middle of an interval
lies close to the middle of an interval  , one can choose between
, one can choose between  and
and  without adding too much distortion. This allows to embed messages under the condition that the receiver does not need to know which positions were modified.
without adding too much distortion. This allows to embed messages under the condition that the receiver does not need to know which positions were modified.
It has been shown that if random codes may seem interesting for their asymptotic behavior, their use leads to solve really hard problems; syndrome decoding and covering radius computation, which are proved to be NP-complete and  -complete, respectively (the
-complete, respectively (the  complexity class includes the NP class) [17, 18]. Moreover, no efficient decoding algorithm is known, even for a small nontrivial family of codes. From a practical point of view, this implies that the related steganographic schemes are too complex to be considered as acceptable for real-life applications. Hence, it is of great interest to have a deeper look at other kinds of codes, structured codes, which are more accessible and lead to efficient decoding algorithms. In this way, some previous papers studied the Hamming code [4, 6, 9], the Simplex code [11], and binary BCH codes [12]. Here, we focus on this latter paper, that pointed out the interest in using codes with deep algebraic structures. The authors distinguish two cases, as previously introduced in [8]. The first one is classical: the embedder modifies any position of the cover-data (a vector which is extracted from the cover-medium, and processed by the encoding scheme), the only constraint being the maximum number of modifications allowed. In this case, they showed that binary BCH codes behave well, but pointed out that choosing the most appropriate code among the BCH family is quite hard, we do not know good complete syndrome decoding algorithms for BCH codes. In the second case, some positions are locked and cannot be used for embedding; this is due to the fact that modifying these positions leads to a degradation of the cover-medium that is noticeable. Hence, in order to remain undetectable, the sender restricts himself to keep these positions and lock them. This case is more realistic. The authors showed that there is a tradeoff between the number of elements that can be locked and the efficiency of the code.
complexity class includes the NP class) [17, 18]. Moreover, no efficient decoding algorithm is known, even for a small nontrivial family of codes. From a practical point of view, this implies that the related steganographic schemes are too complex to be considered as acceptable for real-life applications. Hence, it is of great interest to have a deeper look at other kinds of codes, structured codes, which are more accessible and lead to efficient decoding algorithms. In this way, some previous papers studied the Hamming code [4, 6, 9], the Simplex code [11], and binary BCH codes [12]. Here, we focus on this latter paper, that pointed out the interest in using codes with deep algebraic structures. The authors distinguish two cases, as previously introduced in [8]. The first one is classical: the embedder modifies any position of the cover-data (a vector which is extracted from the cover-medium, and processed by the encoding scheme), the only constraint being the maximum number of modifications allowed. In this case, they showed that binary BCH codes behave well, but pointed out that choosing the most appropriate code among the BCH family is quite hard, we do not know good complete syndrome decoding algorithms for BCH codes. In the second case, some positions are locked and cannot be used for embedding; this is due to the fact that modifying these positions leads to a degradation of the cover-medium that is noticeable. Hence, in order to remain undetectable, the sender restricts himself to keep these positions and lock them. This case is more realistic. The authors showed that there is a tradeoff between the number of elements that can be locked and the efficiency of the code.
This paper is organized as follows. In Section 2, we review the basic setting of coding theory used in steganography. In Section 3, we recall the syndrome coding paradigm, including wet paper codes and active warden. Section 4 presents the classical Reed-Solomon codes and gives details on the necessary tools to use them with syndrome coding, notably the Guruswami-Sudan list decoding algorithm. Section 5 leads to the core of this paper; in Section 5.1, we describe a simple algorithm to use Reed-Solomon codes in an optimal way for wet paper coding, and inSection 5.2 we describe and analyze our proposed algorithm constructed upon the Guruswami-Sudan decoding algorithm.
Before going deeper in the subject, please note that we made the choice to represent vectors as horizontal vectors. For general references to error correcting codes, we orientate the reader toward [19].
2. A Word on Coding Theory
We review here a few concepts relevant to coding theory applications in steganography.
Let  be the finite field with
be the finite field with  elements,
elements,  being a power of some prime number. We consider
being a power of some prime number. We consider  -tuples over
-tuples over  , usually referring to them as words. The classical Hamming weight
, usually referring to them as words. The classical Hamming weight  of a word
of a word  is the number of coordinates that is different from zero, and the Hamming distance
is the number of coordinates that is different from zero, and the Hamming distance  between two words
between two words  denotes the weight of their difference, that is, the number of coordinates in which they differ. We denote by
denotes the weight of their difference, that is, the number of coordinates in which they differ. We denote by  the ball of radius
the ball of radius  centered on
centered on , that is,
, that is,  . Recall that the volume of a ball, that is, the number of its elements does not depend on the center
. Recall that the volume of a ball, that is, the number of its elements does not depend on the center  , and is equal to
, and is equal to  in dimension
in dimension  .
.
A linear code is a vector subspace of
is a vector subspace of  for some integer
for some integer  , called the length of the code. The dimension
, called the length of the code. The dimension  of
of  corresponds to its dimension as a vector space. Hence, a linear code of dimension
corresponds to its dimension as a vector space. Hence, a linear code of dimension  contains
contains  codewords. The two main parameters of codes are their minimal distance and covering radius. The minimal distance of
codewords. The two main parameters of codes are their minimal distance and covering radius. The minimal distance of  is the minimal Hamming distance between two distinct codewords and, since we restrict ourself to linear codes, it is the minimum weight of a nonzero codeword. The minimum distance is closely related to the error correction capacity of the code; a code of minimal distance
is the minimal Hamming distance between two distinct codewords and, since we restrict ourself to linear codes, it is the minimum weight of a nonzero codeword. The minimum distance is closely related to the error correction capacity of the code; a code of minimal distance  corrects any error vector of weight at most
corrects any error vector of weight at most  ; that is, it is possible to recover the original codeword
; that is, it is possible to recover the original codeword  from any
from any  , with
, with  . On the other hand, the covering radius
. On the other hand, the covering radius  is the maximum distance between any word of
is the maximum distance between any word of  and the set of all codewords,
and the set of all codewords,  . A linear code of length
. A linear code of length  , dimension
, dimension  , minimum distance
, minimum distance  and covering radius
and covering radius  is said to be
is said to be  .
.
An important point about linear codes is their matrix description. Since a linear code is a vector space, it can be described by a set of linear equations, usually in the shape of a single matrix, called the parity check matrix . That is, for any  linear code
linear code  , there exists an
, there exists an  matrix
matrix  such that
such that

An important consequence is the notion of syndrome of a word, that uniquely identifies the cosets of the code. A coset of  is a set
is a set  . Two remarks have to be pointed out; first, the cosets of
. Two remarks have to be pointed out; first, the cosets of  form a partition of the ambient space
form a partition of the ambient space  ; second, for any
; second, for any  , we have
, we have  , and each coset can be identified by the value of the syndrome
, and each coset can be identified by the value of the syndrome of its elements
of its elements  denoted here as
denoted here as  .
.
The two main parameters  and
and  have interesting descriptions with respect to syndromes. For any word
have interesting descriptions with respect to syndromes. For any word  of weight at most
of weight at most  , the coset
, the coset  has a unique word of weight at most
has a unique word of weight at most  . Stated differently, if the equation
. Stated differently, if the equation  has a solution of weight
has a solution of weight  , then it is unique. Moreover,
, then it is unique. Moreover,  is maximal for this property to hold. On the other hand, for
is maximal for this property to hold. On the other hand, for  element of
element of  , the equation
, the equation  always has a solution
always has a solution  of weight at most
of weight at most  . Again,
. Again,  is extremal with respect to this property; it is the smallest possible value for this to be true.
is extremal with respect to this property; it is the smallest possible value for this to be true.
A decoding mapping, denoted by  , associates with a syndrome
, associates with a syndrome  a vector
a vector  of Hamming weight less than or equal to
of Hamming weight less than or equal to  , which syndrome is precisely equal to
, which syndrome is precisely equal to  ,
,  and
and  . For our purpose, it is not necessary that
. For our purpose, it is not necessary that  returns the vector
returns the vector  of minimum weight. Please, remark that the effective computation of
of minimum weight. Please, remark that the effective computation of  corresponds to the complete syndrome decoding problem, which is hard.
corresponds to the complete syndrome decoding problem, which is hard.
Finally, we need to construct a smaller code  from a bigger one
from a bigger one  . The operation we need is called shortening; for a fixed set of coordinates
. The operation we need is called shortening; for a fixed set of coordinates  , it consists in keeping all codewords of
, it consists in keeping all codewords of  that have zeros for all positions in
that have zeros for all positions in  and then deleting these positions. Remark that if
and then deleting these positions. Remark that if  has parameters
has parameters  with
with  , then the resulting code,
, then the resulting code,  , has length
, has length  and dimension
and dimension  .
.
3. Syndrome Coding
The behavior of a steganographic algorithm can be sketched in the following way:
-
(1)
a cover-medium is processed to extract a sequence of symbols
 , sometimes called cover-data;
, sometimes called cover-data; -
(2)
 is modified into
is modified into  to embed the message
to embed the message  ;
;  is sometimes called the stego-data;
is sometimes called the stego-data; -
(3)
modifications on
 are translated on the cover-medium to obtain the stego-medium.
are translated on the cover-medium to obtain the stego-medium.
Here, we assume that the detectability of the embedding increases with the number of symbols that must be changed to go from  to
to  (see [6, 20] for some examples of this framework).
(see [6, 20] for some examples of this framework).
Syndrome coding deals with this number of changes. The key idea is to use some syndrome computation to embed the message into the cover-data. In fact, such a scheme uses a linear code  , more precisely its cosets, to hide
, more precisely its cosets, to hide  . A word
. A word  hides the message
hides the message  if
if  lies in a particular coset of
lies in a particular coset of  , related to
, related to  . Since cosets are uniquely identified by the so-called syndromes, embedding/hiding consists exactly in searching
. Since cosets are uniquely identified by the so-called syndromes, embedding/hiding consists exactly in searching  with syndrome
with syndrome  , close enough to
, close enough to  .
.
3.1. Simple Syndrome Coding
We first set up the notation and describe properly the syndrome coding framework and its inherent problems. Let  denote the cover-data and
denote the cover-data and  the message. We are looking for two mappings, embedding
the message. We are looking for two mappings, embedding  and extraction
and extraction  , such that
, such that


Equation (2) means that we want to recover the message in all cases; (3) means that we authorize the modification of at most  coordinates in the vector
coordinates in the vector  .
.
From Section 2, it is quite easy to show that the scheme defined by

enables to embed messages of length  in a cover-data of length
in a cover-data of length  , while modifying at most
, while modifying at most  elements of the cover-data.
elements of the cover-data.
The parameter  represents the (worst) embedding efficiency, that is, the number of embedded symbols per embedding changes in the worst case. In a similar way, one defines the average embedding efficiency
represents the (worst) embedding efficiency, that is, the number of embedded symbols per embedding changes in the worst case. In a similar way, one defines the average embedding efficiency  , where
, where  is the average weight of the output of
is the average weight of the output of  for uniformly distributed inputs. Here, both efficiencies are defined with respect to symbols and not bits. Linking symbols with bits is not simple, as naive solutions lead to bad results in terms of efficiency. For example, if elements of
for uniformly distributed inputs. Here, both efficiencies are defined with respect to symbols and not bits. Linking symbols with bits is not simple, as naive solutions lead to bad results in terms of efficiency. For example, if elements of  are viewed as blocks of
are viewed as blocks of  bits, modifying a symbol roughly leads to
bits, modifying a symbol roughly leads to  bit flips on average and
bit flips on average and  for the worst case.
for the worst case.
3.2. Syndrome Coding with Locked Elements
A problem raised by the syndrome coding, as presented above, is that any position in the cover-data  can be changed. In some cases, it is more reasonable to keep some coordinates unchanged because they would produce too big artifacts in the stego-data. This can be achieved in the following way. Let
can be changed. In some cases, it is more reasonable to keep some coordinates unchanged because they would produce too big artifacts in the stego-data. This can be achieved in the following way. Let  be the coordinates that must not be changed, let
be the coordinates that must not be changed, let  be the matrix obtained from
be the matrix obtained from  by removing the corresponding columns; this matrix defines the shortened code
by removing the corresponding columns; this matrix defines the shortened code  . Let
. Let  and
and  be the corresponding encoding and decoding mappings, that is,
be the corresponding encoding and decoding mappings, that is,  for
for  , and
, and  is a vector of weight at most
is a vector of weight at most  such that its syndrome, with respect to
such that its syndrome, with respect to  , is
, is  . Here,
. Here,  is the covering radius of
is the covering radius of  . Finally, let us define
. Finally, let us define  as the vector of
as the vector of  such that the coordinates in
such that the coordinates in  are zeros and the vector obtained by removing these coordinates is precisely
are zeros and the vector obtained by removing these coordinates is precisely  . Now, we have
. Now, we have  and, by definition,
and, by definition,  has zeros in coordinates lying in
has zeros in coordinates lying in  . Naturally, the scheme defined by
. Naturally, the scheme defined by

performs syndrome coding without disturbing the positions in  . But, it is worth noting that for some sets
. But, it is worth noting that for some sets  , the mapping
, the mapping  cannot be defined for all possible values of
cannot be defined for all possible values of  because the equation
because the equation  has no solution. This always happens when
has no solution. This always happens when  , since
, since  has dimension
has dimension  , but can also happen for smaller sets.
, but can also happen for smaller sets.
3.3. Syndrome Coding for an Active Warden
The previous setting focuses on distortion minimization to avoid detection by the entity inspecting the communication channel, the warden. This supposes the warden keeps a passive role, only looking at the channel. But, the warden can, in a preventive way, modify the data exchanged over the channel. To deal with this possibility, we consider that the stego-data may be modified by the warden, who can change up to  of its coordinates. (In fact, we suppose that the action of the warden on the stego-medium translates onto the stego-data in such a way that at most
of its coordinates. (In fact, we suppose that the action of the warden on the stego-medium translates onto the stego-data in such a way that at most  coordinates are changed.)
coordinates are changed.)
This case has been addressed independently with different strategies by [21, 22]. To address it with syndrome coding, we want  with
with  . This requires that the balls
. This requires that the balls  are disjoint for different messages
are disjoint for different messages  . In fact, the requirements on
. In fact, the requirements on  lead to a known generalization of error correcting codes, called centered error correcting codes (CEC codes). They are defined by an encoding mapping
lead to a known generalization of error correcting codes, called centered error correcting codes (CEC codes). They are defined by an encoding mapping  such that
such that  and the balls
and the balls  do not intersect;
do not intersect;  is precisely what we need for
is precisely what we need for  in the active warden setting. A decoding mapping for this centered code plays the role of
in the active warden setting. A decoding mapping for this centered code plays the role of  .
.
Our problem can be reformulated as follows. Let us consider an error correcting code  of dimension
of dimension  and length
and length  used for syndrome coding, this code having a
used for syndrome coding, this code having a  parity check matrix
parity check matrix  ; now, let us consider a subcode
; now, let us consider a subcode  of
of  , of dimension
, of dimension  , defined by its
, defined by its  parity check matrix
parity check matrix  , which can be written as
, which can be written as

The  additional parity check equations given by
additional parity check equations given by  correspond to the restriction from
correspond to the restriction from  to
to  . The cosets of
. The cosets of  in
in  , that is, the sets
, that is, the sets  , can be indexed in this way
, can be indexed in this way

The equation,  , means that the word
, means that the word  belongs to
belongs to  , and
, and  gives the coset of
gives the coset of  in which
in which  lies. These cosets are pairwise disjoint and their union is
lies. These cosets are pairwise disjoint and their union is  . The index
. The index  may be identified with its binary expansion, and we can identify the embedding step with looking for a word
may be identified with its binary expansion, and we can identify the embedding step with looking for a word  such that
such that

Hence, we can choose  , where
, where  is a solution of
is a solution of  , with
, with  .
.
3.4. A Synthetic View of Syndrome Coding for Steganography
The classical problem of syndrome coding presented in Section 3.1 can be extended in several directions, as presented in Sections 3.2 and 3.3. It is possible to merge both in one to get at the same time reduced distortion and active warden resistance. This has some impact on the parity check matrices we have to consider.
Starting from the setting of the active warden, the problem becomes to find solutions of  , with the additional restriction that
, with the additional restriction that  for
for  . This means that we have to solve a particular instance of syndrome coding with locked elements, the syndrome has a special shape
. This means that we have to solve a particular instance of syndrome coding with locked elements, the syndrome has a special shape  .
.
4. What Reed-Solomon Codes Are, and Why They May Be Interesting
Reed-Solomon codes over the finite field  are optimal linear codes. The narrow-sense RS codes have length
are optimal linear codes. The narrow-sense RS codes have length  and can be defined as a particular subfamily of the BCH codes. But, we prefer the alternative, and larger, definition as an evaluation code, which leads to the generalized Reed-Solomon codes (GRS codes) .
and can be defined as a particular subfamily of the BCH codes. But, we prefer the alternative, and larger, definition as an evaluation code, which leads to the generalized Reed-Solomon codes (GRS codes) .
4.1. Reed-Solomon Codes as Evaluation Codes
Roughly speaking, a GRS code of length  and dimension
and dimension  is a set of words corresponding to polynomials of degree less than
is a set of words corresponding to polynomials of degree less than  evaluated over a subset of
evaluated over a subset of  of size
of size  . More precisely, let
. More precisely, let  be a subset of
be a subset of  and define
and define  where
where  is a polynomial over
is a polynomial over  . Then, we define
. Then, we define  as
as

This definition, a priori, depends on the choice of the  and the order of evaluation; but, as the code properties do not depend on this choice, we will only focus here on the number
and the order of evaluation; but, as the code properties do not depend on this choice, we will only focus here on the number  of
of  and will consider an arbitrary set
and will consider an arbitrary set  and order. Remark that when
and order. Remark that when  with
with  a primitive element of
a primitive element of  and
and  , we obtain the narrow-sense Reed-Solomon codes .
, we obtain the narrow-sense Reed-Solomon codes .
As we said, GRS codes are optimal since they are maximum distance separable (MDS); the minimal distance of  is
is  , which is the largest possible. On the other hand, the covering radius of
, which is the largest possible. On the other hand, the covering radius of  is known and equal to
is known and equal to  .
.
Concerning the evaluation function, recall that if we consider  elements of
elements of  , then it is known that there is a unique polynomial of degree at most
, then it is known that there is a unique polynomial of degree at most  taking particular values on these
taking particular values on these  elements. This means that for every
elements. This means that for every  in
in  , one can find a polynomial
, one can find a polynomial  with
with  , such that
, such that  ; moreover,
; moreover,  is unique. With a slight abuse of notation, we write
is unique. With a slight abuse of notation, we write  . Of course,
. Of course,  is a linear mapping,
is a linear mapping,  for any polynomials
for any polynomials  and field elements
and field elements  .
.
Thus, the evaluation mapping can be represented by the matrix

If we denote by  the vector consisting of the coefficients of
the vector consisting of the coefficients of  , then
, then  . On the other hand,
. On the other hand,  being nonsingular, its inverse
being nonsingular, its inverse  computes
computes  from
from  . For our purpose, it is noteworthy that the coefficients of monomials of degree at least
. For our purpose, it is noteworthy that the coefficients of monomials of degree at least  can be easily computed from
can be easily computed from  , splitting
, splitting  in two parts
in two parts

 is precisely the coefficients vector of the monomials of degree at least
is precisely the coefficients vector of the monomials of degree at least  in
in  . In fact,
. In fact,  is the transpose of a parity check matrix of
is the transpose of a parity check matrix of  , since a vector
, since a vector  is an element of the code if and only if we have
is an element of the code if and only if we have  . So, instead of
. So, instead of  , we write
, we write  , as it is usually done.
, as it is usually done.
4.2. A Polynomial View of Cosets
Now, let us look at the cosets of  . A coset is a set of the type
. A coset is a set of the type  , with
, with  not in
not in  . As usual with linear codes, a coset is uniquely identified by the vector
. As usual with linear codes, a coset is uniquely identified by the vector  , syndrome of
, syndrome of  . In the case of GRS codes, this vector consists of the coefficients of monomials of degree at least
. In the case of GRS codes, this vector consists of the coefficients of monomials of degree at least  .
.
4.3. Decoding Reed-Solomon Codes
4.3.1. General Case
Receiving a vector  , the output of the decoding algorithm may be
, the output of the decoding algorithm may be
-
(i)
a single polynomial
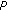 , if it exists, such that the vector
, if it exists, such that the vector 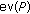 is at distance at most
is at distance at most 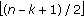 from
from  (remark that if such a
(remark that if such a 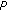 exists, it is unique), and nothing otherwise;
exists, it is unique), and nothing otherwise;
(i i) a list of all polynomials  such that the vectors
such that the vectors  are at distance at most
are at distance at most  from
from  ,
,  being an input parameter.
being an input parameter.
The second case corresponds to the so-called list decoding; an efficient algorithm for GRS codes was initially provided by [23], and was improved by [24], leading to the Guruswami-Sudan (GS) algorithm.
We just set here the outline of the GS algorithm, providing more details in the appendix. The Guruswami-Sudan algorithm uses a parameter called the interpolation multiplicity  . For an input vector
. For an input vector  , the algorithm computes a special bivariate polynomial
, the algorithm computes a special bivariate polynomial  such that each couple
such that each couple  is a root of
is a root of  with multiplicity
with multiplicity  . The second and last step is to compute the list of factors of
. The second and last step is to compute the list of factors of  , of the form
, of the form  , with
, with  . For a fixed
. For a fixed  , the list contains all the polynomials which are at distance at most
, the list contains all the polynomials which are at distance at most  . The maximum decoding radius is, thus,
. The maximum decoding radius is, thus,  . Moreover, the overall algorithm can be performed in less than
. Moreover, the overall algorithm can be performed in less than  arithmetic operations over
arithmetic operations over  .
.
4.3.2. Shortened GRS Case
The Guruswami-Sudan algorithm can be used for decoding shortened GRS codes. For a fixed set  of indices, we are looking for polynomials
of indices, we are looking for polynomials  such that
such that  ,
,  for
for  and
and  for as many
for as many  as possible. Such
as possible. Such  can be written as
can be written as  with
with  . Hence, decoding the shortened code reduces to obtain
. Hence, decoding the shortened code reduces to obtain  such that
such that  and
and  for as many
for as many  as possible. Stated differently, it reduces to decode in
as possible. Stated differently, it reduces to decode in  , which can be done by the GS algorithm.
, which can be done by the GS algorithm.
5. What Can Reed-Solomon Codes Do?
Our problem is the following. We have a vector  of
of  symbols of
symbols of  , extracted from the cover-medium, and a message
, extracted from the cover-medium, and a message  . We want to modify
. We want to modify  into
into  such that
such that  is embedded in
is embedded in  , changing at most
, changing at most  coordinates in
coordinates in  .
.
The basic principle is to use syndrome coding with a GRS code. We use the cosets of a GRS code to embed the message, finding a vector  in the proper coset, close enough to
in the proper coset, close enough to  . Thus, we suppose that we have fixed
. Thus, we suppose that we have fixed  , constructed the matrix
, constructed the matrix  whose
whose  th row is
th row is  , and inverted it. In particular, we denote by
, and inverted it. In particular, we denote by  the last
the last  columns of
columns of  , and therefore, according to Section 4.1,
, and therefore, according to Section 4.1,  is a parity-check matrix. Recall that a word
is a parity-check matrix. Recall that a word  embeds the message
embeds the message  if
if  .
.
To construct  , we need a word
, we need a word  such that its syndrome is
such that its syndrome is  ; thus, we can set
; thus, we can set  , which leads to
, which leads to  . Moreover, the Hamming weight of
. Moreover, the Hamming weight of  is precisely the number of changes we apply to go from
is precisely the number of changes we apply to go from  to
to  ; so, we need
; so, we need  .
.
When  is equal to the covering radius of the code corresponding to
is equal to the covering radius of the code corresponding to  , such a vector
, such a vector  always exists. But, explicit computation of such a vector
always exists. But, explicit computation of such a vector  , known as the bounded syndrome decoding problem, is proved to be NP-hard for general linear codes. Even for families of deeply structured codes, we usually do not have polynomial time (in the length
, known as the bounded syndrome decoding problem, is proved to be NP-hard for general linear codes. Even for families of deeply structured codes, we usually do not have polynomial time (in the length  ) algorithms to solve the bounded syndrome decoding problem up to the covering radius. This is precisely the problem faced by [12].
) algorithms to solve the bounded syndrome decoding problem up to the covering radius. This is precisely the problem faced by [12].
GRS codes overcome this problem in a nice fashion. It is easy to find a vector with syndrome  . Let us consider the polynomial
. Let us consider the polynomial  that has coefficient
that has coefficient  for the monomial
for the monomial  ,
,  ; according to the previous section, we have
; according to the previous section, we have  . Now, finding
. Now, finding  can be done by computing a polynomial
can be done by computing a polynomial  of degree less than
of degree less than  such that for at least
such that for at least  elements
elements  we have
we have  . With such a
. With such a  , the vector
, the vector  has at least
has at least  coordinates equal to zero, and the correct syndrome value. Hence,
coordinates equal to zero, and the correct syndrome value. Hence,  and the challenge lies in the construction of
and the challenge lies in the construction of  .
.
It is noteworthy to remark that locking the position  , that is, requiring
, that is, requiring  , is equivalent to require
, is equivalent to require  and, thus, to ask for
and, thus, to ask for  .
.
5.1. A Simple Construction of P
5.1.1. Using Lagrange Interpolation
A very simple way to construct  is Lagrange interpolation. We choose
is Lagrange interpolation. We choose  coordinates
coordinates  and compute
and compute

where  is the unique polynomial of degree at most
is the unique polynomial of degree at most  taking values
taking values  on
on  ,
,  and
and  on
on  , that is,
, that is,

The polynomial  we obtain by this way clearly satisfies
we obtain by this way clearly satisfies  for any
for any  and, thus, can match
and, thus, can match  . As pointed out earlier, since, for
. As pointed out earlier, since, for  , we have
, we have  , we also have
, we also have  , that is, positions in
, that is, positions in  are locked.
are locked.
The above proposed solution has a nice feature; by choosing  , we can choose the coordinates on which
, we can choose the coordinates on which  and
and  are equal, and this does not require any loss in computational complexity or embedding efficiency. This means that we can perform the syndrome decoding directly with the additional requirement of wet papers keeping unchanged the coordinates whose modifications are detectable.
are equal, and this does not require any loss in computational complexity or embedding efficiency. This means that we can perform the syndrome decoding directly with the additional requirement of wet papers keeping unchanged the coordinates whose modifications are detectable.
5.1.2. Optimal Management of Locked Positions
We can embed  elements of
elements of  , changing not more than
, changing not more than  coordinates, so the embedding efficiency
coordinates, so the embedding efficiency  is equal to
is equal to  in the worst case. But, we can lock any
in the worst case. But, we can lock any positions to embed our information.
positions to embed our information.
This is to be compared with [12], where binary BCH codes are used. In [12], the maximal number of locked positions, without failing to embed the message  , is experimentally estimated to be
, is experimentally estimated to be  . To be able to lock up to
. To be able to lock up to  positions, it is necessary to allow a nonzero probability of nonembedding. It is also noteworthy that the average embedding efficiency decreases fast.
positions, it is necessary to allow a nonzero probability of nonembedding. It is also noteworthy that the average embedding efficiency decreases fast.
In fact, embedding  symbols while locking
symbols while locking  symbols amongst
symbols amongst  is optimal. We said in Section 3 that locking the positions in
is optimal. We said in Section 3 that locking the positions in  leads to an equation
leads to an equation  , where
, where  has dimension
has dimension  . So, when
. So, when  , there exist some values
, there exist some values  for which there is no solution. On the other hand, let us suppose we have a code with parity check matrix
for which there is no solution. On the other hand, let us suppose we have a code with parity check matrix  such that for any
such that for any  of size
of size  , and any
, and any  , this equation has a solution, that is,
, this equation has a solution, that is,  is invertible. This means that any
is invertible. This means that any  submatrix of
submatrix of  is invertible. But, it is known that this is equivalent to require the code to be MDS (see, e.g., [19, Corollary 1.4.14]), which is the case of GRS codes. Hence, GRS codes are optimal in the sense that we can lock as many positions as possible, that is, up to
is invertible. But, it is known that this is equivalent to require the code to be MDS (see, e.g., [19, Corollary 1.4.14]), which is the case of GRS codes. Hence, GRS codes are optimal in the sense that we can lock as many positions as possible, that is, up to  for a message length of
for a message length of  .
.
5.2. A More Efficient Construction of P
If the number of locked positions is less than  , Lagrange interpolation is not optimal since it changes
, Lagrange interpolation is not optimal since it changes  positions, almost always. Unfortunately, Lagrange interpolation is unable to use the additional freedom brought by fewer locked positions.
positions, almost always. Unfortunately, Lagrange interpolation is unable to use the additional freedom brought by fewer locked positions.
A possible way to address this problem is to use a decoding algorithm in order to construct  , that is, we try to decode
, that is, we try to decode  . Locked positions can be dealt with as explained in Section 3.2. If it succeeds, we get a
. Locked positions can be dealt with as explained in Section 3.2. If it succeeds, we get a  in the ball centered on
in the ball centered on  of radius
of radius  , where
, where  is the decoding radius of the decoding algorithm. Here, the Guruswami-Sudan algorithm helps; it provides a large
is the decoding radius of the decoding algorithm. Here, the Guruswami-Sudan algorithm helps; it provides a large  , that is, greater chances of success, and outputs a list of
, that is, greater chances of success, and outputs a list of  which allows to choose the best one with respect to some additional constraints on undetectability. In case of a decoding failure, we can add a new locked position and retry. If we already have
which allows to choose the best one with respect to some additional constraints on undetectability. In case of a decoding failure, we can add a new locked position and retry. If we already have  locked positions, we fall back on Lagrange interpolation.
locked positions, we fall back on Lagrange interpolation.
5.2.1. Algorithm Description
We start with the "while loop" of the algorithm. So suppose that we have a set  of positions to lock. Let
of positions to lock. Let  be the Lagrange interpolation polynomial for
be the Lagrange interpolation polynomial for  , that is,
, that is,  for all
for all  . Thus, we can write
. Thus, we can write  with
with  . We perform a GS decoding on
. We perform a GS decoding on  in
in  , that is, we compute the list of polynomials
, that is, we compute the list of polynomials  such that
such that  and
and

for at least  values
values  , where
, where  is the decoding radius of the GS algorithm, which depends on
is the decoding radius of the GS algorithm, which depends on  and
and  . If the decoding is successful, then
. If the decoding is successful, then  has zeros on positions in
has zeros on positions in  and is equal to
and is equal to  for at least
for at least  positions
positions  . Pick up
. Pick up  such that the distortion induced by
such that the distortion induced by  is as low as possible. Remark that here
is as low as possible. Remark that here  is equal to
is equal to  .
.
The full algorithm (see Algorithm 1) is simply a while loop on the previous procedure, at the end of which, in case of a decoding failure, we add a new position to  . Before commenting the algorithm, let us describe the three external procedures that we use:
. Before commenting the algorithm, let us describe the three external procedures that we use:
-
(i)
the
 procedure outputs a polynomial
procedure outputs a polynomial  such that
such that 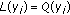 for all
for all 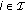 and
and 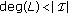 ;
;
(ii) the  procedure refers to the Guruswami-Sudan list decoding (Section 4.3.1). For the sake of simplicity, we just write
procedure refers to the Guruswami-Sudan list decoding (Section 4.3.1). For the sake of simplicity, we just write  for the output list of the GS decoding of
for the output list of the GS decoding of  ,
,  with respect to
with respect to  . So, this procedure returns a good approximation
. So, this procedure returns a good approximation  of
of  , on the evaluation set, of degree less than
, on the evaluation set, of degree less than  ;
;
(iii) the  procedure returns an integer from the set given as a parameter. This procedure is used to choose the new position to lock before retrying list decoding.
procedure returns an integer from the set given as a parameter. This procedure is used to choose the new position to lock before retrying list decoding.
Lines 1 to 5 of the algorithm depicted in Algorithm 1 simply do the setup for the while loop. The while loop, Lines 6 to 12, tries to use list decoding to construct a good solution, as described above. Remark that if all GS decodings fail, we have  with
with  is equal to polynomial
is equal to polynomial  of Section 5.1, that is, we just fall back on Lagrange interpolation. Lines 13 to 16 use the result of the while loop in case of a decoding success, according to the details given above.
of Section 5.1, that is, we just fall back on Lagrange interpolation. Lines 13 to 16 use the result of the while loop in case of a decoding success, according to the details given above.
Correctness of this algorithm follows from the fact that through the whole algorithm we have  and
and  for
for  . Termination is clear since each iteration of the Loop 6-12 increases
. Termination is clear since each iteration of the Loop 6-12 increases  .
.
5.2.2. Algorithm Analysis
The most important property of embedding algorithms is the number of changes introduced during the embedding. Let  be the average number of such changes when GRS
be the average number of such changes when GRS  is used and
is used and  positions are locked. For our algorithm, this quantity depends on two parameters related to the Guruswami-Sudan algorithm:
positions are locked. For our algorithm, this quantity depends on two parameters related to the Guruswami-Sudan algorithm:
Algorithm 1: Algorithm for embedding with locked positions using a  code (
code ( fixed). It embeds
fixed). It embeds  symbols with up to
symbols with up to  locked positions and at most
locked positions and at most  changes.
changes.
Inputs:  , the cover-data
, the cover-data
 , symbols to hide
, symbols to hide
 , set of coordinates to remain unchanged,
, set of coordinates to remain unchanged, 
Output: , the stego-data
, the stego-data
( ;
;  ,
,  ;
;  )
)
-
(1)
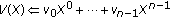
-
(2)
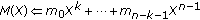
-
(3)
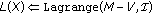
-
(4)
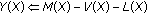
-
(5)
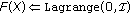
-
(6)
while
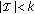 and
and 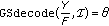 do
do -
(7)

-
(8)
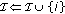
-
(9)
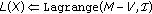
(10) 
(11) 
(12) end while
(1 3) if then
then
(14) 
(15) 
(16) end if
(17) 
(18) return
-
(i)
the probability
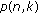 that the list decoding of a word in
that the list decoding of a word in 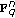 outputs a nonempty list of codewords in GRS
outputs a nonempty list of codewords in GRS 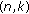 ;
; -
(ii)
the average distance
 between the closest codewords in the (nonempty) list and the word to decode.
between the closest codewords in the (nonempty) list and the word to decode.We denote by
 the probability of an empty list and for conciseness let
the probability of an empty list and for conciseness let 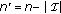 ,
,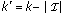 . Thus, the probability that the first
. Thus, the probability that the first 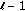 list decodings fail and the
list decodings fail and the  th succeeds can be written as
th succeeds can be written as 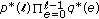 with
with 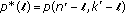 and
and 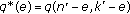 . Remark that in this case,
. Remark that in this case,  coordinates are changed on average.
coordinates are changed on average.
Now, the average number of changes required to perform the embedding can be expressed by the following formula:

-
(a)
Estimating
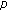 and
and 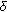
To (upper) estimate  , we proceed as follows. Let
, we proceed as follows. Let  be the random variable equal to the size of the output list of the decoding algorithm. The Markov inequality yields
be the random variable equal to the size of the output list of the decoding algorithm. The Markov inequality yields  , where
, where  denotes the expectation of
denotes the expectation of  . But,
. But,  is the probability that the list is nonempty and, thus,
is the probability that the list is nonempty and, thus,  . Now,
. Now,  is the average number of elements in the output list, but this is exactly the average number of codewords in a Hamming ball of radius
is the average number of elements in the output list, but this is exactly the average number of codewords in a Hamming ball of radius  . Unfortunately, no adequate information can be found in the literature to properly estimate it; the only paper studying a similar quantity is [25], but it cannot be used for our
. Unfortunately, no adequate information can be found in the literature to properly estimate it; the only paper studying a similar quantity is [25], but it cannot be used for our  . So, we set
. So, we set

where  is the volume of a ball of radius
is the volume of a ball of radius  . This would be the correct value if GRS codes were random codes over
. This would be the correct value if GRS codes were random codes over  of length
of length  , with
, with  codewords uniformly drawn from
codewords uniformly drawn from  . That is, we estimate
. That is, we estimate  as if GRS codes were random codes. Thus, we use
as if GRS codes were random codes. Thus, we use  to upper estimate
to upper estimate  .
.
The second parameter we need is  , the average number of changes required when the list is nonempty. We consider that the closest codeword is uniformly distributed over the ball of radius
, the average number of changes required when the list is nonempty. We consider that the closest codeword is uniformly distributed over the ball of radius  and, therefore, we have
and, therefore, we have

-
(b)
Estimating The Average Number of Changes
Using our previous estimations for  and
and  , we plotted
, we plotted  in Figure 1 (
in Figure 1 ( ), Figure 2 (
), Figure 2 ( ), Figure 3 (
), Figure 3 ( ). For each figure, we set
). For each figure, we set  and plotted
and plotted  for several values of
for several values of  .
.
Remember that  and that when
and that when  , our algorithm simply uses Lagrange interpolation, which leads to the maximum number of changes, that is,
, our algorithm simply uses Lagrange interpolation, which leads to the maximum number of changes, that is,  . On the other side, when
. On the other side, when  , our algorithm tries to use Guruswami-Sudan algorithm as much as possible. Therefore, our algorithm improves upon the simpler Lagrange interpolation when
, our algorithm tries to use Guruswami-Sudan algorithm as much as possible. Therefore, our algorithm improves upon the simpler Lagrange interpolation when

is large. A second criterion to estimate the performance is the slope of the plotted curves, the slighter, the better.
With this in mind, looking at Figure 1, we can see that  provides good performances;
provides good performances;  , which means that list decoding avoids up to
, which means that list decoding avoids up to  of the changes required by Lagrange interpolation, and on the other hand, the slope is nearly
of the changes required by Lagrange interpolation, and on the other hand, the slope is nearly  when
when  . For higher embedding rate, all values of
. For higher embedding rate, all values of  less than
less than  have
have  .
.
In Figure 2,  for
for  . In Figure 3,
. In Figure 3,  for
for  , except for
, except for  . Remark that
. Remark that  , the slope is nearly 0 for
, the slope is nearly 0 for  , which means that we can lock about half the coordinates and still have
, which means that we can lock about half the coordinates and still have  of improvement with respect to Lagrange interpolation.
of improvement with respect to Lagrange interpolation.
6. Conclusion
We have shown in this paper that Reed-Solomon codes are good candidates for designing efficient steganographic schemes. They enable to mix wet papers (locked positions) and simple syndrome coding (small number of changes) in order to face not only passive but also active wardens. If we compare them to the previous studied codes, as binary BCH codes, Reed-Solomon codes improve the management of locked positions during embedding, hence ensuring a better management of the distortion; they are able to lock twice the number of positions. Moreover, they are optimal in the sense that they enable to lock the maximal number of positions. We first provide an efficient way to do it through Lagrange interpolation. We then propose a new algorithm based on Guruswami-Sudan list decoding, which is slower but provides an adaptive tradeoff between the number of locked positions and the average number of changes.
In order to use them in real applications, several issues still have to be addressed. First, we need to choose an appropriate measure to properly estimate the distortion induced at the medium level when modifying the symbols at the data level. Second, we need to use a nonbinary, and preferably large, alphabet. A straightforward way to deal with this would be to simply regroup bits to obtain symbols of our alphabet and consider that a symbol should be locked if it contains a bit that should be. Unfortunately, it would lead to a large number of locked symbols (e.g.,  of locked bits leads to up to
of locked bits leads to up to  of locked symbols if we use
of locked symbols if we use  ). A better way would be to use grid coloring [26], keeping a
). A better way would be to use grid coloring [26], keeping a  -to-
-to- ratio. But, the price to this
ratio. But, the price to this  -to-
-to- ratio would be a cut in payload. We think a good solution has yet to be figured out. Nevertheless, in some settings, a large alphabet arises naturally; for example, in [14], a (binary) wet paper code is used on the syndromes of a
ratio would be a cut in payload. We think a good solution has yet to be figured out. Nevertheless, in some settings, a large alphabet arises naturally; for example, in [14], a (binary) wet paper code is used on the syndromes of a  Hamming code, some of these syndromes being locked; here, since whole syndromes are locked, we can view syndromes as elements of the larger field
Hamming code, some of these syndromes being locked; here, since whole syndromes are locked, we can view syndromes as elements of the larger field  and use our proposal. Third, no efficient implementation of the Guruswami-Sudan list decoding algorithm is available. And, as the involved mathematical problems are really tricky, only a specialist can perform a real efficient one. Today, these three issues remain open.
and use our proposal. Third, no efficient implementation of the Guruswami-Sudan list decoding algorithm is available. And, as the involved mathematical problems are really tricky, only a specialist can perform a real efficient one. Today, these three issues remain open.
References
Simmons GJ: The prisoners' problem and the subliminal channel. In Advances in Cryptology. Plenum Press, New York, NY, USA; 1984:51-67.
Böhme R, Westfeld A: Exploiting preserved statistics for steganalysis. In Proceedings of the 6th International Workshop on Information Hiding (IH '04), May 2004, Toronto, Canada, Lecture Notes in Computer Science. Volume 3200. Springer; 82-96.
Franz E: Steganography preserving statistical properties. Proceedings of the 5th International Workshop on Information Hiding (IH '02), October 2002, Noordwijkerhout, The Netherlands, Lecture Notes in Computer Science 2578: 278-294.
Crandall RSome notes on steganography. Posted on steganography mailing list, 1998, http://os.inf.tu-dresden.de/~westfeld/crandall.pdf
Bierbrauer JOn Crandall's problem. Personal communication, 1998, http://www.ws.binghamton.edu/fridrich/covcodes.pdf
Westfeld A: F5—a steganographic algorithm: high capacity despite better steganalysis. Proceedings of the 4th International Workshop on Information Hiding (IH '01), April 2001, Pittsburgh, Pa, USA, Lecture Notes in Computer Science 2137: 289-302.
Galand F, Kabatiansky G: Information hiding by coverings. Proceedings of IEEE Information Theory Workshop (ITW '03), March-April 2003, Paris, France 151-154.
Fridrich J, Goljan M, Lisonek P, Soukal D: Writing on wet paper. IEEE Transactions on Signal Processing 2005, 53(10, part 2):3923-3935.
Fridrich J, Goljan M, Soukal D: Efficient wet paper codes. Proceedings of the 7th International Workshop on Information Hiding (IH '05), June 2005, Barcelona, Spain, Lecture Notes in Computer Science 3727: 204-218.
Fridrich J, Goljan M, Soukal D: Wet paper codes with improved embedding efficiency. IEEE Transactions on Information Forensics and Security 2006, 1(1):102-110. 10.1109/TIFS.2005.863487
Fridrich J, Soukal D: Matrix embedding for large payloads. IEEE Transactions on Information Forensics and Security 2006, 1(3):390-395. 10.1109/TIFS.2006.879281
Schönfeld D, Winkler A: Embedding with syndrome coding based on BCH codes. In Proceedings of the 8th Workshop on Multimedia and Security (MM&Sec '06), September 2006, Geneva, Switzerland. ACM; 214-223.
Schönfeld D, Winkler A: Reducing the complexity of syndrome coding for embedding. In Proceedings of the 9th International Workshop on Information Hiding (IH '07), June 2007, Saint Malo, France, Lecture Notes in Computer Science. Volume 4567. Springer; 145-158.
Zhang W, Zhang X, Wang S: Maximizing steganographic embedding efficiency by combining Hamming codes and wet paper codes. Proceedings of the 10th International Workshop on Information Hiding (IH '08), May 2008, Santa Barbara, Calif, USA, Lecture Notes in Computer Science 5284: 60-71.
Bierbrauer J, Fridrich J: Constructing good covering codes for applications in steganography. In Transactions on Data Hiding and Multimedia Security III, Lecture Notes in Computer Science. Volume 4920. Springer, Berlin, Germany; 2008:1-22. 10.1007/978-3-540-69019-1_1
Fridrich J, Goljan M, Soukal D: Perturbed quantization steganography. ACM Multimedia and Security Journal 2005, 11(2):98-107. 10.1007/s00530-005-0194-3
Vardy A: The intractability of computing the minimum distance of a code. IEEE Transactions on Information Theory 1997, 43(6):1757-1766. 10.1109/18.641542
McLoughlin A: The complexity of computing the covering radius of a code. IEEE Transactions on Information Theory 1984, 30(6):800-804. 10.1109/TIT.1984.1056978
Huffman WC, Pless V: Fundamentals of Error-Correcting Codes. Cambridge University Press, Cambridge, UK; 2003.
Kim Y, Duric Z, Richards D: Modified matrix encoding technique for minimal distortion steganography. In Proceedings of the 8th International Workshop on Information Hiding (IH '06), June 2006, Alexandria, Va, USA, Lecture Notes in Computer Science. Volume 4437. Springe; 314-327.
Galand F, Kabatiansky G: Steganography via covering codes. Proceedings of the IEEE International Symposium on Information Theory (ISIT '03), June-July 2003, Yokohama, Japan 192.
Zhang X, Wang S: Stego-encoding with error correction capability. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences 2005, E88-A(12):3663-3667. 10.1093/ietfec/e88-a.12.3663
Sudan M: Decoding of Reed Solomon codes beyond the error-correction bound. Journal of Complexity 1997, 13(1):180-193. 10.1006/jcom.1997.0439
Guruswami V, Sudan M: Improved decoding of Reed-Solomon and algebraic-geometry codes. IEEE Transactions on Information Theory 1999, 45(6):1757-1767. 10.1109/18.782097
McEliece RJ: The Guruswami-Sudan decoding algorithm for Reed-Solomon codes. In IPN Progress Report. 42-153 California Institute of Technology, Pasadena, Calif, USA; 2003.http://tmo.jpl.nasa.gov/progress_report/42-153/153F.pdf
Fridrich J, Lisonek P: Grid colorings in steganography. IEEE Transactions on Information Theory 2007, 53(4):1547-1549.
von zur Gathen J, Gerhard J: Modern Computer Algebra. 2nd edition. Cambridge University Press, Cambridge, UK; 2003.
Acknowledgments
Dr. C. Fontaine is supported (in part) by the European Commission through the IST Programme under Contract IST-2002-507932 ECRYPT and by the French National Agency for Research under Contract ANR-RIAM ESTIVALE. The authors are in debt to Daniel Augot for numerous comments on this work, in particular for pointing out the adaptation of the Guruswami-Sudan algorithm to shortened GRS used in the embedding algorithm.
Author information
Authors and Affiliations
Corresponding author
A.1. Description
Recall we have a vector  and we want to find all polynomials
and we want to find all polynomials  such that
such that  is at distance at most
is at distance at most  from
from  , and
, and  . We construct a bivariate polynomial
. We construct a bivariate polynomial  over
over  such that
such that  for all
for all  at distance at most
at distance at most  from
from  . Then, we compute all
. Then, we compute all  from a factorization of
from a factorization of  .
.
First, let us define what is called the multiplicity of a zero for bivariate polynomial:  has a zero
has a zero  of multiplicity
of multiplicity  if and only if the coefficients of the monomials
if and only if the coefficients of the monomials  in
in  are equal to zero for all
are equal to zero for all  with
with  . This leads to
. This leads to  linear equations in the coefficients of
linear equations in the coefficients of  . Writing
. Writing  , then
, then  with
with


Since a multiplicity  in
in  is exactly
is exactly  for
for  , and we have
, and we have  values of
values of  and
and  such that
such that  , we have the right number of equations.
, we have the right number of equations.
The principle is to use the  linear equations in the coefficients of
linear equations in the coefficients of  , obtained by requiring
, obtained by requiring  to be a zero of
to be a zero of  with multiplicity
with multiplicity  for
for  . Solving this system leads to the bivariate polynomial
. Solving this system leads to the bivariate polynomial  , but, to be sure our system has a solution, we need more unknowns than equations. To address this point, we impose a special shape on
, but, to be sure our system has a solution, we need more unknowns than equations. To address this point, we impose a special shape on  . For a fixed integer
. For a fixed integer  , we set
, we set  with the restriction that
with the restriction that  . Thus,
. Thus,  has at most
has at most


coefficients. Choosing  such that
such that  guarantees to have nonzero solutions. Of course, since degrees of
guarantees to have nonzero solutions. Of course, since degrees of  must be nonnegative integers, we have
must be nonnegative integers, we have  .
.
On the other hand, under the conditions we imposed on  , one can prove that for all polynomials
, one can prove that for all polynomials  of degree less than
of degree less than  and at distance at most
and at distance at most  from
from  ,
,  divides
divides  . Detailed analysis of the parameters shows it is always possible to take
. Detailed analysis of the parameters shows it is always possible to take  less than or equal to
less than or equal to


(see [19, Chapter 5]). Thus, we have the formula  , which leads to the maximum radius
, which leads to the maximum radius  for
for  large enough.
large enough.
A.2. Complexity
Using  in (A.2), there are
in (A.2), there are  linear equations with roughly
linear equations with roughly  unknowns. Solving these equations with fast general linear algebra can be done in less than
unknowns. Solving these equations with fast general linear algebra can be done in less than  arithmetic operations over
arithmetic operations over  (see [27, Chapter 12]).
(see [27, Chapter 12]).
Finding the factor  can be achieved in a simple way, considering an extension of
can be achieved in a simple way, considering an extension of  of order
of order  . A (univariate) polynomial
. A (univariate) polynomial  over
over  of degree less than
of degree less than  can be uniquely represented by an element
can be uniquely represented by an element  of
of  and, under this representation, to find factors
and, under this representation, to find factors  of
of  is equivalent to find factors
is equivalent to find factors  of
of  , that is, to compute factorization of a univariate polynomial of degree
, that is, to compute factorization of a univariate polynomial of degree  over
over  which can be done in at most
which can be done in at most  operations over
operations over  , neglecting logarithmic factors (see [27, Chapter 14]).
, neglecting logarithmic factors (see [27, Chapter 14]).
The global cost of this basic approach is heavily dominated by the linear algebra part in  with a particularly large degree in
with a particularly large degree in  . It is possible to perform the Guruswami-Sudan algorithm at a cheaper cost, still in
. It is possible to perform the Guruswami-Sudan algorithm at a cheaper cost, still in  , with less naive algorithms. Complete details can be found in [25].
, with less naive algorithms. Complete details can be found in [25].
To sum up, Guruswami-Sudan decoding algorithm finds polynomials  of degree at most
of degree at most  and at distance at most
and at distance at most  from
from  using simple linear algebra and factorization of univariate polynomial over a finite field for a cost in less than
using simple linear algebra and factorization of univariate polynomial over a finite field for a cost in less than  arithmetic operations in
arithmetic operations in  . This can be reduced to
. This can be reduced to  with dedicated algorithms.
with dedicated algorithms.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fontaine, C., Galand, F. How Reed-Solomon Codes Can Improve Steganographic Schemes. EURASIP J. on Info. Security 2009, 274845 (2009). https://doi.org/10.1155/2009/274845
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/274845
 , sometimes called cover-data;
, sometimes called cover-data; is modified into
is modified into  to embed the message
to embed the message  ;
;  is sometimes called the stego-data;
is sometimes called the stego-data; are translated on the cover-medium to obtain the stego-medium.
are translated on the cover-medium to obtain the stego-medium.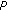 , if it exists, such that the vector
, if it exists, such that the vector 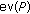 is at distance at most
is at distance at most 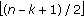 from
from  (remark that if such a
(remark that if such a 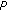 exists, it is unique), and nothing otherwise;
exists, it is unique), and nothing otherwise; procedure outputs a polynomial
procedure outputs a polynomial  such that
such that 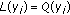 for all
for all 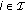 and
and 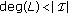 ;
;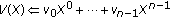
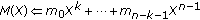
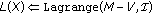
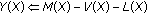
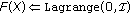
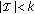 and
and 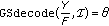 do
do
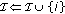
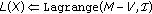
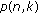 that the list decoding of a word in
that the list decoding of a word in 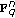 outputs a nonempty list of codewords in GRS
outputs a nonempty list of codewords in GRS 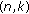 ;
; between the closest codewords in the (nonempty) list and the word to decode.
between the closest codewords in the (nonempty) list and the word to decode. the probability of an empty list and for conciseness let
the probability of an empty list and for conciseness let 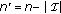 ,
,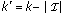 . Thus, the probability that the first
. Thus, the probability that the first 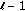 list decodings fail and the
list decodings fail and the  th succeeds can be written as
th succeeds can be written as 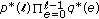 with
with 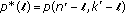 and
and 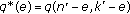 . Remark that in this case,
. Remark that in this case,  coordinates are changed on average.
coordinates are changed on average.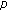 and
and 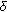

 . Only curves with
. Only curves with  are plotted.
are plotted.
 . Only curves with
. Only curves with  are plotted.
are plotted.
 . Only curves with
. Only curves with are plotted.
are plotted.