- Research Article
- Open access
- Published:
Video Data Hiding for Managing Privacy Information in Surveillance Systems
EURASIP Journal on Information Security volume 2009, Article number: 236139 (2009)
Abstract
From copyright protection to error concealment, video data hiding has found usage in a great number of applications. In this work, we introduce the detailed framework of using data hiding for privacy information preservation in a video surveillance environment. To protect the privacy of individuals in a surveillance video, the images of selected individuals need to be erased, blurred, or re-rendered. Such video modifications, however, destroy the authenticity of the surveillance video. We propose a new rate-distortion-based compression-domain video data hiding algorithm for the purpose of storing that privacy information. Using this algorithm, we can safeguard the original video as we can reverse the modification process if proper authorization can be established. The proposed data hiding algorithm embeds the privacy information in optimal locations that minimize the perceptual distortion and bandwidth expansion due to the embedding of privacy data in the compressed domain. Both reversible and irreversible embedding techniques are considered within the proposed framework and extensive experiments are performed to demonstrate the effectiveness of the techniques.
1. Introduction
Video Surveillance has become a part of our daily lives. Closed-circuit cameras are mounted in countless shopping malls for deterring crimes, at toll booths for assessing tolls, and at traffic intersections for catching speeding drivers. Since the 9–11 terrorist attack, there have been much research efforts directed at applying advanced pattern recognition algorithms to video surveillance. While the objective is to turn the labor intensive surveillance monitoring process into a powerful automated system for counter-terrorism, there is a growing concern that the new technologies can severely undermine individual's rights of privacy. The combination of ubiquitous cameras, wireless connectivity, and powerful recognition algorithms makes it easier than ever to monitor every aspect of our daily activities.
M. W. Hail has conducted a recent survey assessing citizens across demographic groups to see if they were comfortable with the expansion of government video surveillance if it protected privacy rights. (The survey was a cooperative effort through the University of Kentucky annual Kentucky Survey and the research was sponsored by a grant from the US Department of Homeland Security through the National Institute for Hometown Security.) The survey research was conducted utilizing a modified list-assisted Waksberg-Mitofsky random-digit dialing procedure for sampling and the population surveyed was noninstitutionalized Kentuckians eighteen years of age and older. The margin of error is  3.3% at the
3.3% at the  confidence interval. The respondents were asked, "Do you have a video security system that is used routinely?'' The results reflected that
confidence interval. The respondents were asked, "Do you have a video security system that is used routinely?'' The results reflected that  of employed Kentuckians have an operative video surveillance system at their workplace. We then asked of those employed, "Would you be interested in a video surveillance system at work if you knew it could protect an individual's privacy?'' The solid majority of
of employed Kentuckians have an operative video surveillance system at their workplace. We then asked of those employed, "Would you be interested in a video surveillance system at work if you knew it could protect an individual's privacy?'' The solid majority of  expressed that they were interested in privacy protecting video surveillance. Urban residents, those in higher income levels, and those with advanced education attainment all were more disposed to privacy protecting video technology. Additionally, focus groups of law enforcement, first responders, hospitals, and public infrastructure managers have all reflected strong interest in privacy protecting video technology.
expressed that they were interested in privacy protecting video surveillance. Urban residents, those in higher income levels, and those with advanced education attainment all were more disposed to privacy protecting video technology. Additionally, focus groups of law enforcement, first responders, hospitals, and public infrastructure managers have all reflected strong interest in privacy protecting video technology.
To mitigate public's concern on privacy violation, it is thus imperative to make privacy protection a priority in developing new surveillance technologies. There have been many recent work in enhancing privacy protection in surveillance systems [1–8]. Many of them share the common theme of identifying sensitive information and applying image processing schemes for obfuscating that sensitive information. However, the security flaw overlooked in most of these current systems is that they fail to consider the security impact of modifying the surveillance videos. There are a number of security measures that must be incorporated before such modifications can be deployed. Firstly, mechanisms must be in place to authenticate modified videos so that no one can falsify a different modified video by adding and deleting images of objects or individuals. We call this measure privacy data authentication. The second measure is that the original video must be preserved and can only be retrieved under proper authorization. This is of paramount importance to any privacy protection schemes as all schemes are selective in the sense that the sensitive content are intended to a certain group for a certain purpose. No content should be permanently erased. For example, in a corporation, the security camera officer may have access to video contents of all visitors but not the employees; the chief privacy officer will have access to video contents of visitors and all employees except for the executive team but the law enforcement, with a proper order from the court, will have access to the true original footage. It has been postulated that such a static privacy policy would not be sufficient in more sophisticated environments or other sharing applications like teleconference where each participant might need to control the accessibility capability of each consumer of the content as in [9]. We call this measure privacy data preservation.
As explained earlier, except for the simplest organization, merely keeping the original video in encrypted form will not be sufficient in addressing these needs. On the other hand, it is advantageous to reuse the infrastructure of existing standard based video surveillance systems as much as possible. In this work, we propose using video data hiding for preserving the privacy information in the modified video itself in a seamless fashion. Using data hiding, the video bit stream will be accessible for both regular and authorized decoders but only the later can retrieve the hidden privacy information. The use of data hiding for privacy data preservation makes it completely independent from the obfuscation step unlike in some other work [10, 11]. Also, the presence of a single bit stream makes the process of video authentication much simpler to handle. Digitally signing the data hidden bit stream will authenticate the original video as well as all levels of privacy protected data.
From copyright protection to error concealment, video data hiding has found usage in a great number of applications. However, the application of using data hiding for privacy data preservation is unique in the sense it requires huge amount of information to be embedded in the video without disturbing the compression bit syntax. Since data hiding disturbs the underlying statistical patterns of the source data, it adversely affects the performance of compression which are designed based on the statistical properties of the data. As such, it is imperative to design a data hiding scheme that is compatible with the compression algorithm and at the same time, introduces as little perceptual distortion as possible. In this paper, we propose a novel compression-domain video data-hiding algorithm that determines the optimal embedding strategy to minimize both the output perceptual distortion and the output bit rate. The hidden data is embedded into selective Discrete Cosine Transform (DCT) coefficients which are found in most video compression standards. The coefficients are selected based on minimizing a cost function that combines both distortion and bit rate via a user-controlled weighting. Two methods are proposed—exhaustive search and fast Lagrangian approximation. While the former produces optimal results, the latter approach is significantly faster and amenable to real-time implementation. Also two different embedding approaches are discussed. The first approach produces better compression performance but causes irreversible changes even for the authorized decoder while the second approach is both imperceptible to the regular decoder as well as completely reversible to the authorized decoder. However, this additional reversibility comes only at the cost of compression performance as the motion feedback loop can no longer be used and hence this technique can be applied only to intracoded frames or enhancement layers in a scalable codec. This reversible embedding is especially useful in certain applications where the data hiding cannot change the cover data even at a bit level. We can summarize the contributions of this paper as follows.
-
(1)Propose
a Privacy-Protected Video Surveillance System which can authenticate and preserve the privacy information.
-
(2)Propose
a data hiding framework for managing privacy information which can support any kind of video modification.
-
(3)Propose
a compression domain data hiding algorithm which offers high level of hiding capacity by embedding privacy information in selected transform coefficients optimized in terms of distortion and bit-rate.
The rest of the paper is organized as follows. First in Section 2, we briefly review the state-of-the-art in privacy protection and management systems and video data hiding. In Section 3, we describe the higher level design of our privacy protection system and its components. Section 4 introduces the data hiding framework for managing privacy information and various embedding techniques and perceptual distortion and rate models. Keeping the special constraints of data hiding for this application in consideration, we propose the optimization framework to find the embedding locations in Section 5. Experimental results are presented in Section 6 followed by conclusions in Section 7.
2. Related Work
In this section, we review existing work on visual privacy protection technologies followed by video data hiding techniques. There is a recent surge of interest in selective protection of visual objects in video surveillance. The PrivacyCam surveillance system developed at IBM protects privacy by revealing only the relevant information such as object tracks or suspicious activities [8]. Such a system is limited by the types of events it can detect and may have problems balancing privacy protection with the particular needs of a security officer. Alternatively, one can modify the video to obfuscate the appearance of individuals for privacy protection. In [1], the authors propose a privacy protecting video surveillance system which utilizes RFID sensors to identify incoming individuals, ascertains their privacy preference specified in an XML-based privacy policy database, and finally uses a simple video masking technique to selectively conceal authorized individuals and display unauthorized intruders in the video. While [1] may be the first to describe a privacy protected video surveillance system, there are a large body of work that utilize such kinds of video modification for privacy protection. They range from the use of black boxes or large pixels in [2, 3] to complete object removal as in [1]. New techniques have also been proposed recently to replace a particular face with a generic face [6, 12] or a body with a stick figure [7] or complete object removal followed by inpainting of background and other foreground objects [13, 14].
All the afore-mentioned work target only at the modification of the video but not at the feasibility of recovering original video securely. To securely preserve the original video, selective scrambling of sensitive information using a private key have been recently proposed in [10, 11, 15]. These schemes differ in terms of the types of information scrambled which leads to different complexity and compression performances—spatial pixels are scrambled in [10], DCT signs and Wavelet coefficients are used in [11, 15], respectively. With the appropriate private key, the scrambling can be undone to retrieve the original video. These techniques have the advantages of simplicity with modified regions clearly marked. However, there are a number of drawbacks. First, similar to pixelation and blocking, scrambling is unable to fully protect the privacy of individuals, revealing their routes, motion, shape, and even intensity levels [6]. Second, as obfuscation is usually the first step in a complex process chain of a smart surveillance system, it introduces artifacts that can affect the performance of subsequent image processing. Lastly, the coupling of scrambling and data preservation prevents other obfuscation schemes like object replacement or removal to be used.
Using data hiding for privacy data preservation is more flexible as it completely isolates preservation from modification. Since our introduction of using data hiding for privacy data preservation in [16], there have been other work like [9, 17–20] that employ a similar approach. Data hiding has been used in various applications such as copyright protection, authentication, fingerprinting, and error concealment. Each application imposes a different set of constraints in terms of capacity, perceptibility, and robustness [21]. Privacy data preservation certainly demands a large embedding capacity as we are hiding an entire video bitstream in the modified video. Perceptual quality of the embedded video is also of great importance as it effects the usability of the video for further processing. Robustness refers to the survivability of the hidden data under various processing operations. While it is a key requirement for applications like copyright protection and authentication, it is of less concern to a well-managed video surveillance system targeted to serve a single organization. Thus, we are focusing mainly on high-capacity fragile data hiding schemes. Another dimension is the reversibility of the hiding process which dictates if the embedded video can be fully restored after the hidden data is removed. While irreversible data hiding usually produces higher hiding capacity, reversible data hiding may be important for maintaining the authenticity of the original video. We shall consider both in this work.
Most irreversible data embedding and extracting approaches can be classified into two classes—spread spectrum and quantization index modulation (QIM). Spread spectrum techniques treats the data hiding problem as the transmission of the hidden information over a communication channel corrupted by the covered data [22]. QIM techniques use different quantization code-books to represent the covered data with the selection of code-books based on the hidden information [23]. QIM-based techniques usually have higher capacities than spread-spectrum schemes. The capacity of any QIM scheme is determined by the design of the quantization schemes. In [24], the authors propose to hide large volume of information into the nonzero DCT terms after quantization. This method cannot provide sufficient embedding capacity for our application because surveillance videos have high temporal correlation with a very large fraction of DCT coefficients being zero in the intercoded frames. In [25], the authors propose to implement the embedding in both zero and non-zero DCT coefficients but only in macro blocks with low inter frame velocity. This framework deals only with minimizing perceptual distortion without considering the increase in bit rate. Our initial scheme in [16] embeds the watermark bits at the high-frequency DCT coefficients during the compression process. Similar to [25], this method works well in terms of maintaining the output video quality but at an expense of much higher output bit rate.
Reversible data embedding can be broadly classified into three categories. The first class of methods like [26, 27] basically use lossless compression to create space for data hiding. The key idea is to embed the recovery information along with the hidden data to enable the reversibility at the decoder. This method is not suitable for our application because of its low capacity and that the information to be embedded is already a compressed bit stream. The second class of methods like [28, 29] work on residual expansion between pairs of coefficients in various transform domains. These methods assume high correlation between coefficients, hence most of the pairs would not overflow even after expanding the difference. The drawback of these schemes is the higher perceptual distortion caused due to significant changes in coefficient values. The third category of algorithms like [30] work on the concept of histogram bin shifting. This is suitable for our application because the histogram of DCT residue is Laplacian so that we can hide information at small-magnitude coefficients without imposing significant perceptual distortion.
In Section 5, we describe a new approach of optimally placing hidden information in the DCT domain that simultaneously minimizes both the perceptual distortion and output bitrate. Our algorithm considers both rate and distortion and produces an optimal distribution of hidden bits among various DCT blocks. Our main contribution in the data hiding algorithm is an optimization framework to combine both the distortion and rate together as a single cost function and to use it in identifying the optimal locations to hide data. This allows a significant amount of information to be embedded into compressed bitstreams without disproportional increase in either output bit rate or perceptual distortion. This algorithm works for both irreversible and reversible embedding approaches.
3. Privacy Protected Video Surveillance
In order to appreciate the role of privacy data preservation, it is imperative to understand how it fits into the overall architecture of a privacy protected video surveillance system. A high level description of our proposed system is shown in Figure 1 and more details about this system can be found in [31]. The system contains a subject identification module unit which uses RFID tags to identify and discriminate an authorized user from others. The input video from the camera units is processed to identify and extract out the privacy information and the empty regions left behind by the removal of objects are perceptually filled in the Obfuscation Unit using video in-painting as proposed in [14]. The privacy object information is sent to the Secure Data Hiding unit to be encrypted and embedded inside the modified video. This entire process is done within the secure camera system, which is a trusted environment within which raw privacy data or decryption keys are used. All the processing units are connected through an open local area network, and as such, all privacy information must be encrypted before transmission and the identities of all involved units must be validated. The Privacy Data Management System provides the necessary key distribution and privacy policy management so as to support selective and secure recovery of original video based on the status and policy specified by an individual user.
In this paper, we limit our discussion to the data hiding unit used for integrating the privacy information with the modified video. The privacy information contains the image objects of the individuals carrying the RFID tags, each padded with a black background to make a rectangular frame and compressed using a H.263 version 2 video encoder [32]. The embedding process is performed at frame level so that the decoder can reconstruct the privacy information as soon as the compressed bitstream of the same frame has arrived. Before the embedding, the compressed bitstream for each object is encrypted using the Advanced Encryption Standard (AES) with a 128-bit key and appended with a small fixed-size header. Details of the encryption process, key management and the header format can be found in [31]. It is this encrypted data stream that is embedded into the modified video. The data hiding scheme is combined with the video encoder and produces a H.263-compliant bitstream of the protected video to be stored in the database. The privacy protected video can be accessed without any restriction with a standard decoder as all the privacy information are encrypted and hidden in the bitstream. With a special decoder, the hidden data can be retrieved and the authorized user can decrypt the privacy information corresponding to his access level.
4. Hiding Privacy Information
In this section, we describe the various components in our proposed data hiding unit. Figure 2 shows the overall design of the data hiding unit and its interaction with the video compression algorithm. Our data hiding is integrated with a typical motion-compensated DCT video compression algorithm such as H.263. In Figure 2, the purple area contains the components of the data hiding module while the green area contains those of the compression module. There are two inputs to this combined unit: the first one is the Privacy Protected Video with the sensitive information already redacted. The second input is the compressed video bitstreams of the privacy information, encrypted based on the approach described in Section 3. The goal is to hide the second input in the first input in a joint data-hiding compression framework. After the motion compensation process, the residue of the privacy protected video is converted into the DCT domain. The embedding step is introduced between the final step of entropy coding and the DCT. This ensures that the decoder gets the same reference frame to prevent any drifting errors. The encrypted video stream is hidden, using a modified parity embedding scheme, in the luminance DCT blocks which occupy the largest portion of the bit stream. The positions of embedding are obtained using an R-D optimization framework to minimize the distortion and rate increase for a target embedding requirement. The distortion is based on human visual system and a perceptual mask in DCT domain is used to facilitate the calculation. The distortion and rate calculations for the R-D block and the embedding techniques are explained in the following subsections. The full details of the optimization algorithm is given in Section 5. Note that while the proposed data hiding algorithm is general enough to be used in any video codec, the distortion and rate calculations are specific to an H.263 codec.
4.1. Perceptual Distortion
To identify the embedding locations that cause the minimal disturbance to visual quality, we need a distortion metric to input into our optimization framework. Mean square distortion does not work for our goal of finding the optimal DCT coefficients to embed data bits—as DCT is an orthogonal transform, the mean square distortion for the same number of embedded bits will always be the same regardless of which DCT coefficients are used. Instead, we adopt the DCT perceptual model proposed by Watson [33], which has been shown to better correlate with the human visual system than standard mean square distortion. While there are other more sophisticated video-based perceptual models such as the one in [34], we adopt the Watson model for its simplicity to be included in our optimization algorithm.
The Watson model takes into account the overall luminance, contrast and frequency of a coefficient, and calculates a perceptual mask  that indicates the maximum just-noticeable change to
that indicates the maximum just-noticeable change to  , the
, the  th coefficient of the
th coefficient of the  DCT block of an image:
DCT block of an image:

where

for  . Also,
. Also,  is the frequency sensitivity threshold,
is the frequency sensitivity threshold,  is the DC term of block
is the DC term of block  , and
, and  is the average luminance of the image [21]. The higher the mask value, the less distortion the corresponding coefficient will cost by embedding hidden data. As the embedding is performed in the quantized coefficient domain, it is convenient to normalize with the quantization step-size and use the following distortion value instead:
is the average luminance of the image [21]. The higher the mask value, the less distortion the corresponding coefficient will cost by embedding hidden data. As the embedding is performed in the quantized coefficient domain, it is convenient to normalize with the quantization step-size and use the following distortion value instead:

where QP is the quantization parameter and  is the perceptual mask value as calculated in (1). As a few highly distorted coefficients account for more distortion than many mildly distorted ones [21], an
is the perceptual mask value as calculated in (1). As a few highly distorted coefficients account for more distortion than many mildly distorted ones [21], an  norm pooling is employed for calculating the total distortion over the entire frame:
norm pooling is employed for calculating the total distortion over the entire frame:

4.2. Irreversible Embedding Process
To embed data in the compressed bitstream, we follow the QIM approach in which quantization is altered based on the hidden data. Let  and
and  be the
be the  -th coefficient of the
-th coefficient of the  th DCT block before and after quantization, respectively. They are related as in (5) where QP is the chosen quantization parameter at the codec:
th DCT block before and after quantization, respectively. They are related as in (5) where QP is the chosen quantization parameter at the codec:

The maximum error due to the quantization will be QP as reconstruction values are centered in the quantization bins of width  . To enable the data hiding, the quantization is made coarser with the finer levels reserved to represent the embedded bits. To embed an
. To enable the data hiding, the quantization is made coarser with the finer levels reserved to represent the embedded bits. To embed an  -bit number
-bit number  in a coefficient, the quantized coefficient can be altered in two different ways:
in a coefficient, the quantized coefficient can be altered in two different ways:

or

The choice of embedding with (6) or (7) depends on which method produces a reconstructed value closer to the real  . Hidden data extraction is straightforward—for an
. Hidden data extraction is straightforward—for an  -bit embedding in a particular coefficient, it is given as in (8):
-bit embedding in a particular coefficient, it is given as in (8):

This embedding, however, is not invertible. Since the quantization is altered to a coarser level as part of data embedding, it causes irrecoverable loss of data. For a single bit embedding, the maximum quantization noise doubles compared to that of without embedding. Beside the irreversible changes to the coefficient, the modified reference frame in the motion loop propagates the effect of data hiding into future frames, making the changes permanent. This implies that the reconstructed video will be slightly different from the originally compressed version. Such an irreversible embedding method is not suitable for certain applications that demand the original video to be unaltered by the data hiding process.
4.3. Reversible Embedding Process
Using the previous embedding technique, the decoder has no way to remove the distortion introduced by the embedding process. In this subsection, we explain a reversible embedding algorithm whose effect can be reversed on the decoder side after data extraction. A key requirement for our application is that the output bit-stream with hidden data must be decodable with good quality by a standard-compliant decoder unaware of the embedding. This implies that we need to avoid any error caused by drifting and as such, the decoded frame with the hidden data must be used in the feedback path in the motion loop. As the motion compensation does not respect the DCT block boundary, the effect of hiding one bit in a DCT coefficient may spread to different spatial areas after many frames. It is an open question on how to make this temporal spreading reversible. In our current implementation, we focus on making the DCT embedding process reversible and prevent temporal spreading by restricting our attention to either intracoded frames or intracoded-enhanced frames in a two-layer scalable codec.
The reversible embedding algorithm exploits the fact that DCT coefficients follow a Laplacian distribution concentrated around zero with empty bins towards either ends of the distribution [30]. Due to the high concentration at the zero bin, we can embed high-volume of hidden data at the zero coefficients by shifting the bins right (or left) of zero to the right (or left). At the encoder side, the embedding process is as follows: let  be the number of bits to be hidden in the
be the number of bits to be hidden in the  th quantized DCT block. Let
th quantized DCT block. Let  where
where  is the number of zero coefficients in this DCT block. In a dynamic order specified by optimization algorithm, we modify each DCT coefficients
is the number of zero coefficients in this DCT block. In a dynamic order specified by optimization algorithm, we modify each DCT coefficients  into
into  using the following procedure until all the
using the following procedure until all the  bits of privacy data are embedded. Notice that we have
bits of privacy data are embedded. Notice that we have  and
and  and
and  is the DCT block index.
is the DCT block index.
-
(1)If
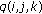 is zero, extract
is zero, extract 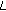 bits from the privacy data buffer and set
bits from the privacy data buffer and set  where
where 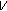 is the decimal value of these
is the decimal value of these 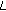 privacy data bits.
privacy data bits. -
(2)If
 is negative, no embedding is done and
is negative, no embedding is done and  .
. -
(3)If
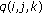 is positive, no embedding is done and
is positive, no embedding is done and 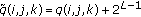 .
.
The embedding is done only at zero coefficients while all the other coefficients visited in the scan order are displaced in either positive or negative direction. Compared with the irreversible embedding, the capacity here is smaller as data can only be embedded to zero coefficients. Also reversible embedding induces higher distortion as even some nonzero coefficients must be altered by  without actually embedding at that position.
without actually embedding at that position.
On the decoder side, it needs to extract the hidden bits and retrieve the original quantized coefficient  from
from  . The decoder also knows the number of hidden bits
. The decoder also knows the number of hidden bits  by running the same rate distortion algorithm. To find the number of coefficients that contain the hidden data, the decoder determines the minimum
by running the same rate distortion algorithm. To find the number of coefficients that contain the hidden data, the decoder determines the minimum  such that
such that  where
where  is the number of DCT coefficients satisfying the condition
is the number of DCT coefficients satisfying the condition  . Following the block specific pattern given by the optimization algorithm, the privacy data and the original DCT coefficient can be obtained as follows.
. Following the block specific pattern given by the optimization algorithm, the privacy data and the original DCT coefficient can be obtained as follows.
-
(1)If
 ,
, 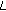 hidden bits can be obtained as the binary equivalent of the decimal number
hidden bits can be obtained as the binary equivalent of the decimal number  and
and 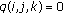 .
. -
(2)If
 , no bit is hidden in this coefficient and
, no bit is hidden in this coefficient and 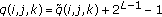 .
. -
(3)If
 , no bit is hidden in this coefficient and
, no bit is hidden in this coefficient and 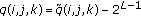 .
.
4.4. Rate Model
Data hiding effects the compression performance—simply choosing the distortion-optimal locations based on the perceptual model may increase the output bit-rate manyfold. As surveillance video is typically quite static, many DCT blocks do not have any non-zero coefficients. Hiding bits into these zero blocks, while perceptual optimal, may significantly increase the bit-rate. This is caused by the fragmentation of the long run-length patterns which are assumed to be frequent by the entropy coder. One possible approach to mitigate this problem is to limit the number of blocks to be modified [16]. However, the fewer blocks used for embedding, the more spatially concentrated the embedding becomes which will make the distortion more visible. As such, we need to measure the increase in rate by different embedding strategies so as to produce the optimal tradeoff with the distortion. The rate increase for a particular embedding is calculated using the actual entropy coder used for compression. As both the encoder and the decoder need to compute the rate function so as to derive the optimal data hiding positions, the actual privacy data cannot be used as it is not available at the decoder. Instead, we approximate the embedding by assuming the "worst-case'' embedding, that is, we choose the hidden bit value that causes the higher increase in bit-rate.
5. Rate-Distortion-Optimized Data Hiding
In our joint data hiding and compression framework, we aim at minimizing the output bit rate  and the perceptual distortion
and the perceptual distortion  caused by embedding
caused by embedding  bits into the DCT coefficients. By using a user-specified control parameter
bits into the DCT coefficients. By using a user-specified control parameter  , we combine the rate and distortion into a single cost function as follows:
, we combine the rate and distortion into a single cost function as follows:

where  is a constant used to equalize the dynamic ranges of
is a constant used to equalize the dynamic ranges of  and
and  so that varying
so that varying  translates to trading-off between
translates to trading-off between  and
and  . As such,
. As such,  is not a free parameter and is determined based on the particular compression mechanism. On the other hand, the choice of
is not a free parameter and is determined based on the particular compression mechanism. On the other hand, the choice of  depends on applications—it is selected based on the particular application which may favor the least amount of distortion by setting
depends on applications—it is selected based on the particular application which may favor the least amount of distortion by setting  close to zero, or the least amount of bit rate increase by setting
close to zero, or the least amount of bit rate increase by setting  close to one. In order to avoid any overhead in communicating the embedding positions to the decoder, both of these approaches compute the optimal positions based on the previously decoded DCT frame so that the process can be repeated at the decoder. In our data hiding framework, the constrained optimization can be formulated as follows:
close to one. In order to avoid any overhead in communicating the embedding positions to the decoder, both of these approaches compute the optimal positions based on the previously decoded DCT frame so that the process can be repeated at the decoder. In our data hiding framework, the constrained optimization can be formulated as follows:

where  is the variable that denotes the number of coefficients to be modified,
is the variable that denotes the number of coefficients to be modified,  is the target number of bits to be embedded,
is the target number of bits to be embedded,  is the cost function as described in (9), and
is the cost function as described in (9), and  is any selection of
is any selection of  DCT coefficients for embedding the data. We assume that a constant number of bits are embedded at each DCT coefficient and focus the optimization on choosing the coefficients for embedding (with the exception of the last DCT coefficient for embedding which may contain less than the target number). While it is entirely feasible to explore the dimension of embedding different numbers of bits to different coefficients, our preliminary experiments indicate that the gain is too small to justify the significant expansion of the search space for the optimization.
DCT coefficients for embedding the data. We assume that a constant number of bits are embedded at each DCT coefficient and focus the optimization on choosing the coefficients for embedding (with the exception of the last DCT coefficient for embedding which may contain less than the target number). While it is entirely feasible to explore the dimension of embedding different numbers of bits to different coefficients, our preliminary experiments indicate that the gain is too small to justify the significant expansion of the search space for the optimization.
Lagrangian method turns a constrained optimization problem like (10) into an unconstrained one, and is commonly used in rate-distortion optimized video compression. Using a Lagrange Multiplier  , the constrained optimization problem introduced in (10) can be turned into an unconstrained version:
, the constrained optimization problem introduced in (10) can be turned into an unconstrained version:

If the unconstrained problem (11) for a particular  has an optimal solution that gives rise to
has an optimal solution that gives rise to  , this will also be a solution to the original constrained problem [35]. We can further simplify (11) by decomposing it into the sum of similar quantities from each DCT block
, this will also be a solution to the original constrained problem [35]. We can further simplify (11) by decomposing it into the sum of similar quantities from each DCT block  :
:


where  denotes the particular selection of
denotes the particular selection of  coefficient in the
coefficient in the  th DCT block and
th DCT block and  is the total number of DCT blocks in a frame. The minimization can now be performed for each block at different values of
is the total number of DCT blocks in a frame. The minimization can now be performed for each block at different values of  so as to make
so as to make  . There are two subproblems here. First, while the second term on the right side in (13) is constant for a particular value of
. There are two subproblems here. First, while the second term on the right side in (13) is constant for a particular value of  , the minimization of the first term is not trivial. In other words, we need to find an optimal subset of
, the minimization of the first term is not trivial. In other words, we need to find an optimal subset of  coefficients in the
coefficients in the  th DCT block to minimize the cost:
th DCT block to minimize the cost:

The second problem is an efficient way to search for  that provides an optimal allocation of embedded bits to each block. The following two subsections describe our approach in tackling these problems.
that provides an optimal allocation of embedded bits to each block. The following two subsections describe our approach in tackling these problems.
5.1. Cost Function Computation for DCT Blocks
There are two components to the cost function introduced in (9): distortion and rate increase due to data hiding. Our distortion function as described in (4) is additive with each coefficient having an independent contribution. The rate increase due to the modification of a coefficient is far more complex. It depends on neighboring coefficients as consecutive coefficients along the zigzag scan are encoded together as a single run-length pattern. In the H.263 standard, a run-length pattern is defined as a run of zero coefficients followed by a nonzero coefficient. The length of the run and the nonzero coefficient determine the length of the codeword, and the longer the run-length, the shorter the codeword in the Huffman table becomes. Embedding a bit in any zero coefficients will break the run-length pattern into two and the bit-rate increase will depend on the original and the resulting run-length patterns.
At first glance, the interdependency created by the run-length coding seems to evade any structural exploitation of the optimization problem. Exhaustive search of  patterns, where
patterns, where  is the number of candidate coefficients and
is the number of candidate coefficients and  is the number of embedded bits, seems inevitable. For a
is the number of embedded bits, seems inevitable. For a  DCT block, such an exhaustive search will need to encode more than
DCT block, such an exhaustive search will need to encode more than  patterns in order to determine all the optimal positions for embedding
patterns in order to determine all the optimal positions for embedding  bits. This is clearly impossible in practice. Fortunately, the "worst-case'' embedding assumption in our rate model as described in Section 4.4 provides a Dynamic-Programming- (DP-) based solution to the optimization problem. In the actual embedding procedure as described in (6) and (7), embedding a specific bit may turn a nonzero DCT coefficient into zero and actually reduces the bit-rate by making a run-length pattern longer. The "worst-case'' embedding, which is employed without the knowledge of the hidden bit, assumes the worst case and never makes a nonzero coefficient zero. This simple observation enables us to develop a recursive solution to the optimization problem based on the position of the last embedded bit.
bits. This is clearly impossible in practice. Fortunately, the "worst-case'' embedding assumption in our rate model as described in Section 4.4 provides a Dynamic-Programming- (DP-) based solution to the optimization problem. In the actual embedding procedure as described in (6) and (7), embedding a specific bit may turn a nonzero DCT coefficient into zero and actually reduces the bit-rate by making a run-length pattern longer. The "worst-case'' embedding, which is employed without the knowledge of the hidden bit, assumes the worst case and never makes a nonzero coefficient zero. This simple observation enables us to develop a recursive solution to the optimization problem based on the position of the last embedded bit.
Let  denotes the minimum cost of embedding
denotes the minimum cost of embedding  bits into a DCT block with the last bit embedded at the
bits into a DCT block with the last bit embedded at the th DCT coefficient along the zigzag scan. Clearly, the optimal cost
th DCT coefficient along the zigzag scan. Clearly, the optimal cost  of embedding
of embedding  bits in this block can be found by the following equation:
bits in this block can be found by the following equation:

(since the approach of computing the cost function is the same for each block, we drop the block index  in representing the block cost function
in representing the block cost function  ).
).
Here we assume all 64 coefficients are available for embedding which is the case for irreversible embedding. For reversible embedding, we can simply limit our candidates to the zero coefficients. With the worst-case embedding, the embedding pattern that realizes  must have a non-zero
must have a non-zero  th DCT coefficient. Denote
th DCT coefficient. Denote  to be the embedding position of the
to be the embedding position of the  st embedded bit. Since the
st embedded bit. Since the  th DCT coefficient must also be non-zero, the run-length patterns before and after the
th DCT coefficient must also be non-zero, the run-length patterns before and after the  th coefficients are independently coded. Let
th coefficients are independently coded. Let  be the cost induced by the run-length patterns between the
be the cost induced by the run-length patterns between the  th and
th and  th coefficients. We can now compute
th coefficients. We can now compute  using the following recursion:
using the following recursion:

This is precisely the Bellman principle that leads to a dynamic programming formulation to solve for  [36]. Now we can state the full algorithm to compute
[36]. Now we can state the full algorithm to compute  for
for  as follows.
as follows.
(1)There are 64 stages with each stage representing the embedding of one bit. At stage  where
where  , there are
, there are  states representing all possible DCT coefficients in the zigzag order that can store the
states representing all possible DCT coefficients in the zigzag order that can store the  th embedded bit. The minimum cost function
th embedded bit. The minimum cost function  will be computed at stage
will be computed at stage  and state
and state  . The trellis depicting this construction is shown in Figure 3.
. The trellis depicting this construction is shown in Figure 3.
(2)The calculation starts from stage one. At stage  , we compute the cost function at state
, we compute the cost function at state  by first worst-case embedding a bit at the
by first worst-case embedding a bit at the  th coefficient and then identifying the minimum combined cost among all the states up to
th coefficient and then identifying the minimum combined cost among all the states up to  in stage
in stage  plus the extra cost incurred by the embedding at the
plus the extra cost incurred by the embedding at the  th coefficient.
th coefficient.
(3)Finally, the minimum cost of embedding  bits can be calculated by minimizing over all the states in stage
bits can be calculated by minimizing over all the states in stage  .
.
To compute the complexity of this DP algorithm, we note that 64 DCT coding patterns are examined in the first stage,  in the second stage,
in the second stage,  in the third and so forth. Altogether one needs to examine 43 744 different DCT encoding patterns to determine the minimum cost embedding. While this is a significant reduction from the naive exhaustive search, encoding one single DCT blocks so many times is still formidable in practice. In our experiments, we have also investigated two more strategies in computing the block cost function: the greedy approximation and a fixed heuristic order within a DCT block. Greedy embedding calculates one optimal embedding location at a time ignoring the complex rate dependencies while heuristic approach takes a fixed reverse zig-zag scan order from the end of the DCT block. Table 1 summarizes the differences in the number DCT patterns examined among all the approaches.
in the third and so forth. Altogether one needs to examine 43 744 different DCT encoding patterns to determine the minimum cost embedding. While this is a significant reduction from the naive exhaustive search, encoding one single DCT blocks so many times is still formidable in practice. In our experiments, we have also investigated two more strategies in computing the block cost function: the greedy approximation and a fixed heuristic order within a DCT block. Greedy embedding calculates one optimal embedding location at a time ignoring the complex rate dependencies while heuristic approach takes a fixed reverse zig-zag scan order from the end of the DCT block. Table 1 summarizes the differences in the number DCT patterns examined among all the approaches.
5.2. Bit Allocation by Lagrangian Approximation
Sweeping through  from
from  to
to  will examine the convex hull of all the block cost functions
will examine the convex hull of all the block cost functions  . While there exist efficient tree pruning techniques to search for the optimal value
. While there exist efficient tree pruning techniques to search for the optimal value  , the large number of DCT blocks in a frame can still render such techniques computationally intensive. As we will demonstrate in Section 6, the block cost functions in most cases can be well approximated by a second order curve. This allows us to devise a simple search strategy to quickly identify the appropriate value of
, the large number of DCT blocks in a frame can still render such techniques computationally intensive. As we will demonstrate in Section 6, the block cost functions in most cases can be well approximated by a second order curve. This allows us to devise a simple search strategy to quickly identify the appropriate value of  .
.
If one can approximate  function as a differentiable function in the continuous domain
function as a differentiable function in the continuous domain  , then the optimal solution to (13) must satisfy the so-called "equal-slope'' criteria:
, then the optimal solution to (13) must satisfy the so-called "equal-slope'' criteria:

for all  . However, (17) implies that the optimal solution exists at a constant equal slope of
. However, (17) implies that the optimal solution exists at a constant equal slope of  for all block cost functions. At an equal slope on all the individual cost funcions, the rate of increase or decrease in cost with respect to the bits embedded will be the same. Hence, we need to search for such constant slope over all the curves which satisfy the total target embedding requirement. Approximating each cost function as a second-order polynomial yields
for all block cost functions. At an equal slope on all the individual cost funcions, the rate of increase or decrease in cost with respect to the bits embedded will be the same. Hence, we need to search for such constant slope over all the curves which satisfy the total target embedding requirement. Approximating each cost function as a second-order polynomial yields

The optimal slope that satisfies our embedding constraint can thus be obtained as follows:

To meet the minimum embedding constraint, the total number of bits embedded from each DCT block must be equal to  :
:

Thus,  can be determined as follows:
can be determined as follows:

Since the actual problem is a discrete one, we can only use  from (21) as an initial slope and search for the exact slope in its neighborhood to match our target embedding requirement. At this optimal slope on each curve, we can identify the number of embedding locations
from (21) as an initial slope and search for the exact slope in its neighborhood to match our target embedding requirement. At this optimal slope on each curve, we can identify the number of embedding locations  for each DCT block. These
for each DCT block. These  embedding locations within each block are chosen from the same optimal order which are already calculated during the cost cuve generation process.
embedding locations within each block are chosen from the same optimal order which are already calculated during the cost cuve generation process.
6. Experiments
We have tested our proposed schemes on six sequences using a variety of video obfuscation techniques. These sequences include the following.
-
Minnesota [37]. Two persons walk towards and cross each other while the camera is slowly panning (39 frames).
-
Board. One person walk across the scene, briefly occluded by a partition board (101 frames).
-
Two-persons. Two persons walk towards and cross each other (89 frames).
-
Three-persons. Two persons walk towards the right and one to the left, occluding each other briefly (73 frames).
-
Conference. Five persons sit around a conference table with two leaving one after the other (356 frames).
-
Hall. A standard sequence used in video compression (299 frames).
All sequences are in CIF ( ) format in YCbCr color space with
) format in YCbCr color space with  sub-sampling. The first four sequences are captured at 15 Hz and the hall monitor is at 30 Hz. For each sequence, privacy objects are extracted according to a separate segmentation mask. The segmentation mask of Minnesota is provided by the authors of [37] and that of Board is manually obtained. The remainders are calculated using the background subtraction and object segmentation schemes described in [14]. The experiments assume all the privacy objects are compressed together in the same privacy bitstream. In practice, multiple persons in the scene would result in multiple bitstreams which will add complexity and payload to the whole process. Using MPEG-4 object-based coding can certainly reduce this payload requirement. Complexity can be reduced by parallelizing the compression of different objects. Three video obfuscation techniques are then applied after the privacy objects are removed. They are (a) silhouette in which the holes are replaced by black pixels, (b) scrambled in which the pixel values are exclusive-OR with a pseudo-random sequence, and (c) in-painted using an object-based video in-painting scheme from [14]. The original sequences, privacy objects and obfuscated sequences are shown in Figure 4 and are available for download at the authors' website (http://www.vis.uky.edu/~cheung/datahiding/).
sub-sampling. The first four sequences are captured at 15 Hz and the hall monitor is at 30 Hz. For each sequence, privacy objects are extracted according to a separate segmentation mask. The segmentation mask of Minnesota is provided by the authors of [37] and that of Board is manually obtained. The remainders are calculated using the background subtraction and object segmentation schemes described in [14]. The experiments assume all the privacy objects are compressed together in the same privacy bitstream. In practice, multiple persons in the scene would result in multiple bitstreams which will add complexity and payload to the whole process. Using MPEG-4 object-based coding can certainly reduce this payload requirement. Complexity can be reduced by parallelizing the compression of different objects. Three video obfuscation techniques are then applied after the privacy objects are removed. They are (a) silhouette in which the holes are replaced by black pixels, (b) scrambled in which the pixel values are exclusive-OR with a pseudo-random sequence, and (c) in-painted using an object-based video in-painting scheme from [14]. The original sequences, privacy objects and obfuscated sequences are shown in Figure 4 and are available for download at the authors' website (http://www.vis.uky.edu/~cheung/datahiding/).
The data hiding algorithm is implemented based on the TMN Coder Version 3.0 of the ITU-T H.263 version 2 by University of British Columbia. All sequences are compressed using a constant quantization parameter with the first frame intracoded and the remaining intercoded. Despite the differences in the original frame-rates among the sequences, the compression frame rate has been set to 30 Hz. The encoding performance is measured based on running the program on a Windows XP Professional machine with Intel Xeon Processor at 2 GHz with 4 GB memory.
6.1. Selection of DCT Coefficients for Embedding
In the first experiment, we consider the performances among different schemes in selecting DCT coefficients to embed hidden data. The three tested schemes are the DP-based optimal scheme, the greedy scheme and the fixed reversed zigzag patterns as described in Section 5.
Figure 5 shows a typical graph of the cost function versus the number of bits embedded within a single DCT block for each of the three schemes. (The graphs show the results of the 100th DCT block from the Minnesota in-painted sequence but the trend is typical among all sequences we have tested.) The cost function is computed according to (9) with  and
and  . For a fixed number of hidden bits, the zigzag scheme clearly produces worse results than both the greedy and the DP-based schemes. The greedy and the DP-based schemes however produce very similar results. The corresponding curves are almost convex which strongly suggests the optimality in using the discrete Lagrangian optimization for allocating hidden bits among different blocks. In addition, the curves can be well approximated by a quadratic curve as shown in the Figure 5, hence justifying the approximation we have introduced in Section 5.2.
. For a fixed number of hidden bits, the zigzag scheme clearly produces worse results than both the greedy and the DP-based schemes. The greedy and the DP-based schemes however produce very similar results. The corresponding curves are almost convex which strongly suggests the optimality in using the discrete Lagrangian optimization for allocating hidden bits among different blocks. In addition, the curves can be well approximated by a quadratic curve as shown in the Figure 5, hence justifying the approximation we have introduced in Section 5.2.
To further demonstrate the differences among these schemes, we have run them on four different in-painted sequences to their entirety, focusing only on the irreversible embedding with the quantization parameter fixed at  . For all the DP-based, greedy, and zigzag schemes, we use the discrete Lagrangian-based bit allocation method as described in Section 5.2. Table 2 summarizes the comparisons in terms of the resulting bitrate after compression with embedding, the average luma PSNR after compression and embedding, the perceptual distortion as defined in (4), the average cost over the entire sequence, and the encoding speed in seconds per frame. There are relatively little differences among the three schemes in bitrate and PSNR. The zigzag scheme produces higher distortion and cost while the DP-based and the greedy schemes produce very similar results as expected. On the other hand, the encoding speeds are exactly the opposite—the DP-based scheme needs around 895 seconds per frame, the greedy scheme needs 35 seconds, and the zigzag needs only 1.5 second. Due to the high computational complexity of the DP-based scheme, we focus on using the greedy scheme rather than the DP-based approach for the remaining experiments.
. For all the DP-based, greedy, and zigzag schemes, we use the discrete Lagrangian-based bit allocation method as described in Section 5.2. Table 2 summarizes the comparisons in terms of the resulting bitrate after compression with embedding, the average luma PSNR after compression and embedding, the perceptual distortion as defined in (4), the average cost over the entire sequence, and the encoding speed in seconds per frame. There are relatively little differences among the three schemes in bitrate and PSNR. The zigzag scheme produces higher distortion and cost while the DP-based and the greedy schemes produce very similar results as expected. On the other hand, the encoding speeds are exactly the opposite—the DP-based scheme needs around 895 seconds per frame, the greedy scheme needs 35 seconds, and the zigzag needs only 1.5 second. Due to the high computational complexity of the DP-based scheme, we focus on using the greedy scheme rather than the DP-based approach for the remaining experiments.
We should point out that the computational speeds provided in Table 2 are based on a nonoptimized implementation of the algorithms and also include the entire compression process, which amounts to roughly 0.6 second. Significant speedup can be achieved, for example, by updating only those blocks that are different from the previous frames as indicated by the macroblock modes. In fact, as the motion in typical surveillance videos is scarce, it is conceivable to update the cost function only occasionally rather than at every frame without losing much optimality. Furthermore, the complexity is mainly due to the computation of the cost functions for different DCT blocks which are certainly amenable to parallel implementation. While it is not the focus of this paper on the real-time implementation of the data hiding process, we believe that significant improvement in computational speed is indeed possible.
6.2. Bit Allocation for DCT Blocks
Our optimization process is a combination of two steps—bit allocation between blocks and choosing optimal the positions within blocks as explained in Sections 5.2 and 5.1, respectively. While the first experiment focuses on different approaches of embedding within a single block, we consider in the second experiment the effect of different approaches in allocating bits among different blocks. To minimize the impact of data hiding on visual quality, [16] divides hidden data equally among all the blocks in the residual frame. We compare this scheme with the proposed Lagrangian approach and the results are shown in Table 3. To ensure a fair comparison, we fix the greedy approach with  to enforce a full emphasis on minimizing the visual distortion. While the equal distribution can indeed provide smaller distortion, the major difference lies in the reduction of bandwidth. On average there is a bandwidth savings of 47% when switching from equal distribution to the Lagrangian approach.
to enforce a full emphasis on minimizing the visual distortion. While the equal distribution can indeed provide smaller distortion, the major difference lies in the reduction of bandwidth. On average there is a bandwidth savings of 47% when switching from equal distribution to the Lagrangian approach.
6.3. Different Privacy Protection Schemes
In the third experiment, we contrast the performances of the greedy scheme over different privacy protection schemes. As one of the key advantages of data hiding for privacy data preservation is its universal applicability to different obfuscation schemes, it is of interest to consider their performances. We have run the greedy irreversible scheme with  for all 6 videos at three different obfuscation schemes. Table 4 summarizes the results. The first row shows the luma PSNR of the sequences after the embedding and compression. While using a constant quantizer would have produced constant quality in a normal video encoder, the presence of hidden data degrades the quality and affects the overall PSNR. The variations in PSNR can be better interpreted using the percentage drop as compared with those of the encoded sequences without hidden data. Also the percentage drop allows us to compare the impact of data embedding across different obfuscation techniques which produce very different video sequences. These numbers are shown in the second row—the large drop in PSNR in Minnesota, Two-persons, and Three-persons is due to the large amount of hidden data caused by the dynamically moving foreground objects. The lower PSNR drop in the scrambled versions compared with the other two is due to the concentration of the hidden data among the high spatial-temporal frequency scrambled areas. In a typical residual frame, most DCT coefficients are close to zero and those coefficients enjoy little distortion due to quantization. Hiding data in these zero coefficients statistically causes a higher relative decrease in PSNR when compared with nonzero coefficients. The scrambling process introduces many non-zero high frequency coefficients that attract hidden data, thus reducing the amount of loss in PSNR as compared to the silhouette and in-painted schemes. These high-frequency coefficients are chosen because they introduce less perceptual distortion, as indicated in the measurements in the third row. On the other hand, these high-frequency coefficients are very difficult to compress. The resulting bitrates after data hiding as shown in the fourth row clearly demonstrate this phenomenon. Similar to PSNR, we also consider the relative increase in bitrates as compared with those of compressing the modified videos and privacy data separately. While it is expected that the hidden data introduces minor or even negative bitrate increase in scrambled videos, there are significant increases in bitrate among silhouette and in-painted sequences—they range from 26% to more than 100%. These increases are more significant among the in-painted sequences than the silhouette sequences. To understand these increases, we calculate the ratio of bitrates of the mark (hidden data) to the cover work (obfuscated video without hidden data) in the last row. It is observed that the bitrate increase correlates well with this ratio. The highest three increases in bitrate correspond to the bitrate ratios larger than one, that is, the hidden data is in fact larger in size than the obfuscated video. This violates a typical assumption used in most data hiding schemes and it is quite conceivable that our scheme operates less than efficient in such an extraordinary condition.
for all 6 videos at three different obfuscation schemes. Table 4 summarizes the results. The first row shows the luma PSNR of the sequences after the embedding and compression. While using a constant quantizer would have produced constant quality in a normal video encoder, the presence of hidden data degrades the quality and affects the overall PSNR. The variations in PSNR can be better interpreted using the percentage drop as compared with those of the encoded sequences without hidden data. Also the percentage drop allows us to compare the impact of data embedding across different obfuscation techniques which produce very different video sequences. These numbers are shown in the second row—the large drop in PSNR in Minnesota, Two-persons, and Three-persons is due to the large amount of hidden data caused by the dynamically moving foreground objects. The lower PSNR drop in the scrambled versions compared with the other two is due to the concentration of the hidden data among the high spatial-temporal frequency scrambled areas. In a typical residual frame, most DCT coefficients are close to zero and those coefficients enjoy little distortion due to quantization. Hiding data in these zero coefficients statistically causes a higher relative decrease in PSNR when compared with nonzero coefficients. The scrambling process introduces many non-zero high frequency coefficients that attract hidden data, thus reducing the amount of loss in PSNR as compared to the silhouette and in-painted schemes. These high-frequency coefficients are chosen because they introduce less perceptual distortion, as indicated in the measurements in the third row. On the other hand, these high-frequency coefficients are very difficult to compress. The resulting bitrates after data hiding as shown in the fourth row clearly demonstrate this phenomenon. Similar to PSNR, we also consider the relative increase in bitrates as compared with those of compressing the modified videos and privacy data separately. While it is expected that the hidden data introduces minor or even negative bitrate increase in scrambled videos, there are significant increases in bitrate among silhouette and in-painted sequences—they range from 26% to more than 100%. These increases are more significant among the in-painted sequences than the silhouette sequences. To understand these increases, we calculate the ratio of bitrates of the mark (hidden data) to the cover work (obfuscated video without hidden data) in the last row. It is observed that the bitrate increase correlates well with this ratio. The highest three increases in bitrate correspond to the bitrate ratios larger than one, that is, the hidden data is in fact larger in size than the obfuscated video. This violates a typical assumption used in most data hiding schemes and it is quite conceivable that our scheme operates less than efficient in such an extraordinary condition.
6.4. Different Operating Parameters
In the fourth experiment, we ran our data hiding algorithm under varying design parameters like QP and  . This is carried out on the two longer sequences: "Hall'' and "Conference'' using inpainting as the obfuscation scheme. Irreversible embedding is examined in this section and reversible embedding in the following section. Four QP parameters are used: 5, 10, 15, and 20 and three
. This is carried out on the two longer sequences: "Hall'' and "Conference'' using inpainting as the obfuscation scheme. Irreversible embedding is examined in this section and reversible embedding in the following section. Four QP parameters are used: 5, 10, 15, and 20 and three  values are used: 0, 0.5, and 1. QP defines the quantization parameter of the codec for compressing both the modified video and privacy information while
values are used: 0, 0.5, and 1. QP defines the quantization parameter of the codec for compressing both the modified video and privacy information while  is the control parameter between rate and distortion during the optimization. However,
is the control parameter between rate and distortion during the optimization. However,  gives the distortion based optimization ignoring rate increase while
gives the distortion based optimization ignoring rate increase while  minimizes only the rate increase during the selection of embedding coefficients. Tables 5 and 6 summarize the results for both sequences. The notations
minimizes only the rate increase during the selection of embedding coefficients. Tables 5 and 6 summarize the results for both sequences. The notations  ,
,  and
and  denote the rates of obfuscated (inpainted) bit stream, privacy bit stream and embedded bit stream, respectively. From the tables, we can observe, as expected, that the rate increase reduces while the perceptual distortion increases with an increase in the control parameter
denote the rates of obfuscated (inpainted) bit stream, privacy bit stream and embedded bit stream, respectively. From the tables, we can observe, as expected, that the rate increase reduces while the perceptual distortion increases with an increase in the control parameter  . Despite the increase in the bitrates of the privacy streams, the percentages of bitrate increase in the embedded stream stay the same or drop at higher QP's due to the presence of more nonzero coefficients that are more suitable for hiding data. Also, the results from both the sequences confirm that PSNR is not a good measure for the cost computation as it does not vary much with parameter
. Despite the increase in the bitrates of the privacy streams, the percentages of bitrate increase in the embedded stream stay the same or drop at higher QP's due to the presence of more nonzero coefficients that are more suitable for hiding data. Also, the results from both the sequences confirm that PSNR is not a good measure for the cost computation as it does not vary much with parameter  , while the perceptual distortion measure better correlates with it. Figure 6 highlights the better visual correlation of the perceptual distortion measure compared to PSNR for the embedding of same hidden information at different locations by using
, while the perceptual distortion measure better correlates with it. Figure 6 highlights the better visual correlation of the perceptual distortion measure compared to PSNR for the embedding of same hidden information at different locations by using  versus
versus  . Figure 7 shows a sample frame from Hall-Monitor sequence before and after irreversible embedding at variable values of QP and
. Figure 7 shows a sample frame from Hall-Monitor sequence before and after irreversible embedding at variable values of QP and  .
.
6.5. Reversible Embedding
The same experiment with varying QP and  is also repeated for the case of reversible embedding. As introduced in Section 4.3, the reversible embedding can only be used when there is no interdependency between the frames. Though the embedding is done in a reversible fashion, the prediction loop used in intercoded frames propagate the effect of hidden data to future frames making the process irreversible. Hence this experiment is conducted in two special encoder structures. In the first structure, each frame is coded using intra mode (I frame) only. This setting is similar to the M-JPEG standard typically found in many IP cameras. The privacy information is also encoded in the same fashion as we assume that the system only has access to a codec which has no capabilities of temporal prediction. In the second structure, we operate the embedding process over the enhanced intra frames (EI frames) of a scalable codec. We use the SNR scalability to derive the enhancement layers. The base layer is always coded at QP = 20 and the enhancement layers are generated to achieve the desired quantization effect. Table 7 summarizes the encoding performances of the two structures at different coding parameters for hall monitor and sequence. As observed from the table, the EI-frame structure yields better results in terms of percentage rate increase and perceptual distortion when compared to embedding in intra frames (I frames). Figure 8 shows a sample frame from Conference before and after reversible embedding on intracoded frames at variable values of QP and
is also repeated for the case of reversible embedding. As introduced in Section 4.3, the reversible embedding can only be used when there is no interdependency between the frames. Though the embedding is done in a reversible fashion, the prediction loop used in intercoded frames propagate the effect of hidden data to future frames making the process irreversible. Hence this experiment is conducted in two special encoder structures. In the first structure, each frame is coded using intra mode (I frame) only. This setting is similar to the M-JPEG standard typically found in many IP cameras. The privacy information is also encoded in the same fashion as we assume that the system only has access to a codec which has no capabilities of temporal prediction. In the second structure, we operate the embedding process over the enhanced intra frames (EI frames) of a scalable codec. We use the SNR scalability to derive the enhancement layers. The base layer is always coded at QP = 20 and the enhancement layers are generated to achieve the desired quantization effect. Table 7 summarizes the encoding performances of the two structures at different coding parameters for hall monitor and sequence. As observed from the table, the EI-frame structure yields better results in terms of percentage rate increase and perceptual distortion when compared to embedding in intra frames (I frames). Figure 8 shows a sample frame from Conference before and after reversible embedding on intracoded frames at variable values of QP and  .
.
7. Conclusions
In this paper, we have presented a privacy-protecting video surveillance system which offers multiple levels of secure privacy information preservation. Novel irreversible and reversible data hiding methods have been proposed to hide large amount of privacy information into the host video. An optimization framework has been proposed to identify DCT coefficients for hiding information that simultaneously minimize the perceptual distortion and the rate increase caused due to embedded information. Extensive experimental results have been presented to demonstrate the efficient implementation of our algorithms and their effectiveness in preserving privacy data.
References
Wickramasuriya J, Datt M, Mehrotra S, Venkatasubramanian N: Privacy protecting data collection in media spaces. Proceedings of the 12th ACM International Conference on Multimedia, October 2004, New York, NY, USA 48-55.
Berger AM: Privacy mode for acquisition cameras and camcorders. US patent 6067399, Sony Corporation, May 2000
Wada J, Kaiyama K, Ikoma K, Kogane H: Monitor camera system and method of displaying picture from monitor camera thereof. European patent, EP 1081955 A2, Matsushita Electric Industrial, April 2001
Schiff J, Meingast M, Mulligan D, Sastry S, Goldberg K: Respectful cameras: detecting visual markers in real-time to address privacy concerns. Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS '07), April 2007, Beijing, China 971-978.
Chen D, Chang Y, Yan R, Yang J: Tools for protecting the privacy of specific individuals in video. EURASIP Journal on Advances in Signal Processing 2007, 2007:-9.
Newton EM, Sweeney L, Main B: Preserving privacy by de-identifying face images. IEEE Transactions on Knowledge and Data Engineering 2005, 17(2):232-243. 10.1109/TKDE.2005.32
Wactlar H, Stevens S, Ng T: Enabling personal privacy protection preferences in collaborative video observation. NSF Award Abstract 0534625, http://www.nsf.gov/awardsearch/showAward.do
Senior A, Pankanti S, Hampapur A, Brown L, Tian Y-L, Ekin A: Blinkering surveillance: enabling video privacy through computer vision. Security and Privacy 2005, 3: 50-57. 10.1109/MSP.2005.65
Cheung S-C, Paruchuri JK, Nguyen T: Managing privacy data in pervasive camera networks. Proceedings of the 15th IEEE International Conference on Image Processing (ICIP '08), October 2008, San Diego, Calif, USA
Boult TE: Pico: privacy through invertible cryptographic obscuration. In Proceedings of the Computer Vision for Interactive and Intelligent Environments, November 2005, The Dr. Bradley D. Carter Workshop Series Edited by: Bradley DC. 27-38.
Dufaux F, Ebrahimi T: Scrambling for video surveillance with privacy. Proceedings of the Conference on Computer Vision and Pattern Recognition Workshop (CVPRW '06), June 2006, New York, NY, USA 160.
Yu X, Babaguchi N: Privacy preserving: hiding a face in a face. Proceedings of the 8th Asian Conference on Computer Vision (ACCV '07), November 2007, Tokyo, Japan, Lecture Notes in Computer Science 4844: 651-661.
Cheung S-C, Zhao J, Venkatesh MV: Efficient object-based video inpainting. Proceedings of the IEEE International Conference on Image Processing (ICIP '06), October 2006, Atlanta, Ga, USA 705-708.
Venkatesh MV, Cheung S-C, Zhao J: Efficient object based video inpainting. Pattern Recognition Letters 2009, 30(2):168-179. 10.1016/j.patrec.2008.03.011
Martin K, Plataniotis KN: Privacy protected surveillance using secure visual object coding. IEEE Transactions on Circuits and Systems for Video Technology 2008, 18: 1152-1162. 10.1109/TCSVT.2008.927110
Zhang W, Cheung S-C, Chen M: Hiding privacy information in video surveillance system. Proceedings of the 12th IEEE International Conference on Image Processing (ICIP '05), September 2005, Genova, Italy
Yu X, Babaguchi N: Hiding a Face in a Face, Lecture Notes in Computer Science. Volume 4844. Springer, Heidelberg, Berlin; 2007.
Li G, Ito Y, Yu X, Nitta N, Babaguchi N: A discrete wavelet transform based recoverable image processing for privacy protection. Proceedings of the International Conference on Image Processing (ICIP '08), 2008 1372-1375.
Paruchuri JK, Cheung S-C: Joint optimization of data hiding and video compression. Proceedings of the IEEE International Symposium on Circuists and Systems (ISCAS '08), May 2008, Washington, DC, USA
Meuel P, Chaumont M, Puech W: Data hiding in h.264 video for lossless reconstruction of region of interest. In Proceedings of the 15th European Signal Processing Conference (EUSIPCO '07), September 2007, Poznan, Poland. HAL—CCSD; 120-124.
Cox I, Miller M, Bloom J: Digital Watermarking. Morgan Kaufmann, San Fransisco, Calif, USA; 2002.
Cox I, Kilian J, Leighton T, Shamoon T: Secure spread spectrum watermarking for multimedia. IEEE Transactions on Image Processing 1997, 6(12):1673-1687. 10.1109/83.650120
Chen B, Wornell GW: Quantization index modulation: a class of provably good methods for digital watermarking and information embedding. Proceedings of the IEEE International Symposium on Information Theory (ISIT '00), June 2000, Sorrento, Italy
Solanki K, Jacobsen N, Chandrasekaran S, Madhow U, Manjunath B: High-volume data hiding in images: introducing perceptual criteria into quantization based embedding. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '02), May 2002, Orlando, Fla, USA 4: 3485-3488.
Sur A, Mukherjee J: Adaptive data hiding in compressed video domain. Proceedings of the Indian Conference on Computer Vision, Graphics and Image Processing (ICVGIP '06), 2006 738-748.
Celik MU, Sharma G, Tekalp AM, Saber E: Lossless generalized-lsb data embedding. IEEE Transactions on Image Processing 2005, 14(2):253-266. 10.1109/TIP.2004.840686
Goljan M, Fridrich J, Du R: Distortion-free data embedding for images. Proceedings of the 4th International Workshop on Information Hiding, 2001, Pittsburgh, Pa, USA 27-41.
Alattar AM: Reversible watermark using the difference expansion of a generalized integer transform. IEEE Transactions on Image Processing 2004, 13(8):1147-1156. 10.1109/TIP.2004.828418
Thodi D, Rodriguez J: Reversible watermarking by prediction-error expansion. Proceedings of the 6th IEEE Southwest Symposium on Image Analysis and Interpretation (SSIAI '04), September 2004, Porto, Portugal 6: 21-25.
Chang CC, Tai WL, Lin MH: A reversible data hiding scheme with modified side match vector quantization. Proceedings of the 19th International Conference on Advanced Information Networking and Applications (AINA '05), March 2005, Taipei, Taiwan 1: 947-952.
Cheung S-C, Venkatesh MV, Paruchuri JK, Zhao J, Nguyen T: Protecting and managing privacy information in video surveillance systems. In Protecting Privacy in Video Surveillance. Springer, New York, NY, USA; 2009.
Video Coding for Low Bitrate Communication Version 2, ITU-T Recommendation H.263 Version 2, 1998
Watson A: Dct quantization matrices optimized for individual images. Human Vision, Visual Processing, and Digital Display IV, October 1993, Proceedings of SPIE 1913: 202-216.
Seshadrinathan K, Bovik AC: A structural similarity metric for video based on motion models. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '07), May 2007, Honolulu, Hawaii, USA 1: 869-872.
Shoham Y, Gersho A: Efficient bit allocation for an arbitrary set of quantizers. IEEE Transactions on Acoustics, Speech, and Signal Processing 1988, 36(9):1445-1453. 10.1109/29.90373
Bellman R: On the theory of dynamic programming. Proceedings of the National Academy of Sciences 1952, 38(8):716-719. 10.1073/pnas.38.8.716
Patwardhan KA, Sapiro G, Bertalmio M: Video inpainting under constrained camera motion. IEEE Transactions on Image Processing 2007, 16(2):545-553. 10.1109/TIP.2006.888343
Acknowledgments
The authors would like to acknowledge the support from Department of Justice for this work and also thank the anonymous reviewers for their constructive comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Paruchuri, J., Cheung, Sc. & Hail, M. Video Data Hiding for Managing Privacy Information in Surveillance Systems. EURASIP J. on Info. Security 2009, 236139 (2009). https://doi.org/10.1155/2009/236139
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/236139


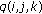 is zero, extract
is zero, extract  bits from the privacy data buffer and set
bits from the privacy data buffer and set  where
where 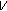 is the decimal value of these
is the decimal value of these 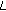 privacy data bits.
privacy data bits. is negative, no embedding is done and
is negative, no embedding is done and  .
.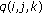 is positive, no embedding is done and
is positive, no embedding is done and 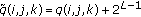 .
. ,
, 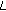 hidden bits can be obtained as the binary equivalent of the decimal number
hidden bits can be obtained as the binary equivalent of the decimal number  and
and 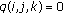 .
. , no bit is hidden in this coefficient and
, no bit is hidden in this coefficient and 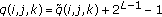 .
. , no bit is hidden in this coefficient and
, no bit is hidden in this coefficient and 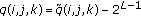 .
.




