- Research Article
- Open access
- Published:
Stochastic Image Warping for Improved Watermark Desynchronization
EURASIP Journal on Information Security volume 2008, Article number: 345184 (2008)
Abstract
The use of digital watermarking in real applications is impeded by the weakness of current available algorithms against signal processing manipulations leading to the desynchronization of the watermark embedder and detector. For this reason, the problem of watermarking under geometric attacks has received considerable attention throughout recent years. Despite their importance, only few classes of geometric attacks are considered in the literature, most of which consist of global geometric attacks. The random bending attack contained in the Stirmark benchmark software is the most popular example of a local geometric transformation. In this paper, we introduce two new classes of local desynchronization attacks (DAs). The effectiveness of the new classes of DAs is evaluated from different perspectives including perceptual intrusiveness and desynchronization efficacy. This can be seen as an initial effort towards the characterization of the whole class of perceptually admissible DAs, a necessary step for the theoretical analysis of the ultimate performance reachable in the presence of watermark desynchronization and for the development of a new class of watermarking algorithms that can efficiently cope with them.
1. Introduction
Geometric transformations whereby the watermark embedder and detector are desynchronized are known to be one of the most serious threats against any digital watermarking scheme. In the case of still images, for which desynchronization attacks (DAs) can be easily implemented by applying a geometric transformation to the watermarked image, DAs are of the outmost importance, since failing to cope with them would nullify the efficacy of the whole watermarking system.
In the general case, a geometric distortion can be seen as a transformation of the position of the pixels in the image. It is possible to distinguish between global and local geometric distortions. A global transformation is defined by an analytic function that maps the points in the input image to the corresponding points in the output image. It is defined by a set of operational parameters and performed over all the image pixels. Local distortions, instead, refer to transformations affecting in different ways the position of the pixels of the same image or affecting only part of the image. The random bending attack [1], contained in the Stirmark utility, is the most famous example of a local geometric transformation.
Global geometric transformations, especially rotation, scaling, and translation, have been extensively studied in the watermarking literature given their simplicity and diffusion. Though no perfect solution exists to cope with geometric attacks, DAs based on global transformations can be handled in a variety of ways, including exhaustive search [2, 3], template-based resynchronization [4–6], self-synchronizing watermarks [7, 8], and watermarking in invariant domains [9]. In all the cases, the proposed solutions rely on the restricted number of parameters specifying the DA. For instance, it is the relatively low cardinality of the set of possible attacks that makes the estimation of the geometric transformation applied by the attacker via exhaustive search or template matching possible (computationally feasible). For this reason, recovering from localized attacks is much harder than recovering from a global attack. A possibility to overcome this problem in case of local attacks could split the search into a number of local searches. However, in this way, it is likely that the accuracy of the estimation is reduced, given that the estimation would have to rely on a reduced number of samples.
Despite the threats they pose, local geometric transformations have received little attention by the watermarking community. In practice, only the random bending sttack (RBA) contained in the Stirmark software has been studied to some extent. However, even in this case, the real de-synchronization capabilities of RBA are not fully understood, given that as implemented in Stirmark, RBA consists of three modules with only one corresponding to a truly local geometric transformation [1].
In this paper, we focus on local geometric attacks for still images. In particular, the aim of our research is twofold:
-
(i)
to introduce two new classes of local DAs that extend the class of local geometric attacks for still images;
-
(ii)
to evaluate the effectiveness of the new attacks and compare them with the classical RBA.
For the above goals, the perceptual impact of the DAs is taken into account since this is the only factor limiting the choice of the attacking strategy. The two models we propose can be seen as a first step towards the characterization of the whole class of perceptually admissible DAs, which in turn is an essential step towards the development of a new class of watermarking systems that can effectively cope with them.
This paper is organized as follows. In Section 2, we describe the RBA contained in the Stirmark software. In Section 3, we introduce a new class of local desynchronization attacks, the LPCD DAs, applied in a full and multiresolution framework. In Section 4, a class of attacks based on Markov random fields is presented. In Section 5, we evaluate the effectiveness of the two new classes of DAs using two simple watermarking systems based on the DCT and DWT transforms. Finally, in Section 6, we summarize the contribution of this work and propose some ideas for future research.
In order to ensure the reproducibility of the experimental results the software, we used for the experiments is available on the web site http://www.dii.unisi.it/~vipp, furthermore a pseudocode description of the algorithms is provided in order to link the software to the global description of the algorithms.
2. Stirmark Rba
The Stirmark benchmark software first explored RBA's ability to confuse watermark detection. In most of the scientific literature, by RBA, the corresponding geometric attack implemented in the Stirmark software is meant [10], however such an attack is not a truly local attack since it couples three different geometric transformations applied sequentially, only the last of which corresponds to a local attack.
The first transformation applied by Stirmark is defined by

where  are the new coordinates and
are the new coordinates and  the old ones. In practice, this transformation corresponds to moving the four corners of the image into four new positions, and modifying coherently all the other sampling positions. The second step is given by
the old ones. In practice, this transformation corresponds to moving the four corners of the image into four new positions, and modifying coherently all the other sampling positions. The second step is given by

where  and
and  are the vertical and horizontal dimensions of the image. This transformation applies a displacement which is zero at the border of the image and maximum (
are the vertical and horizontal dimensions of the image. This transformation applies a displacement which is zero at the border of the image and maximum (  ) in the center. The third step of the Stirmark geometric attack is expressed as
) in the center. The third step of the Stirmark geometric attack is expressed as

where  and
and  are two frequencies (usually smaller than 1/20) that depend on the image size, and
are two frequencies (usually smaller than 1/20) that depend on the image size, and  and
and  are random numbers in the interval
are random numbers in the interval  . However, (3) is the only local component of the Stirmark attack since it introduces a random displacement at every pixel position. In the sequel by RBA, we will mean only the transformation expressed by (3). This can be obtained by using the Stirmark software setting to
. However, (3) is the only local component of the Stirmark attack since it introduces a random displacement at every pixel position. In the sequel by RBA, we will mean only the transformation expressed by (3). This can be obtained by using the Stirmark software setting to  the
the  , and
, and  parameters (resp., the bending factor, the maximum variation of a pixel value, the maximum distance a corner can move inwards and outwards), and leaving
parameters (resp., the bending factor, the maximum variation of a pixel value, the maximum distance a corner can move inwards and outwards), and leaving  (the randomisation factor) to the default value of
(the randomisation factor) to the default value of  .
.
3. The Class of Lpcd Das
In this section, we describe a first new class of DAs, namely, local permutation with cancelation and duplication (LPCD) DAs. We start from the plain LPCD attack, then we pass to the C-LPCD (constrained LPCD). Finally, we consider the multiresolution extension of the above two classes.
3.1. Lpcd
By focusing on the 1D case, let  be a generic signal, and let
be a generic signal, and let  be the distorted version of
be the distorted version of  . The LPCD model states that
. The LPCD model states that  , where
, where  is a sequences of i.i.d random variables uniformly distributed in a predefined interval
is a sequences of i.i.d random variables uniformly distributed in a predefined interval  . For simplicity, we assume that
. For simplicity, we assume that  can take only integer values in
can take only integer values in  . This way, the values assumed by the samples of
. This way, the values assumed by the samples of  are chosen among those of
are chosen among those of  . The above model yields an interesting interpretation of the attacked signal
. The above model yields an interesting interpretation of the attacked signal  . To introduce it, it is convenient to describe the LPCD attack as a channel
. To introduce it, it is convenient to describe the LPCD attack as a channel  defined as follows (neglecting edge effects):
defined as follows (neglecting edge effects):

where (i)  , for
, for  , denotes
, denotes  (a similar notation convention applies to
(a similar notation convention applies to  ), and (ii)
), and (ii)

where  denotes the indicator function of the event
denotes the indicator function of the event  . According to the above equation, the LPCD channel
. According to the above equation, the LPCD channel  assigns the same probability,
assigns the same probability,  , and independently, to all possible values of
, and independently, to all possible values of  , and it picks
, and it picks  . However, any other probability assignment
. However, any other probability assignment  is allowed. Likewise, the probability law of
is allowed. Likewise, the probability law of  does not need to be known (except the fact that it is memoryless). An equivalent representation of this model is obtained by defining
does not need to be known (except the fact that it is memoryless). An equivalent representation of this model is obtained by defining  . Here, if
. Here, if  are i.i.d., then
are i.i.d., then  is a first-order Markov process. Also, the channel
is a first-order Markov process. Also, the channel  from
from  to
to  is obviously memoryless according to (4). Thus,
is obviously memoryless according to (4). Thus,  is governed by a hidden Markov process:
is governed by a hidden Markov process:

The above interpretation of the LPCD model may open the way to the definition of optimum embedding and detection strategies along the same lines described in [11].
To extend the 1D-LPCD model to the two-dimensional case, if  is a generic pixel of the distorted image
is a generic pixel of the distorted image  , we let
, we let

where  is the original image and
is the original image and  and
and  are i.i.d. integer random variables uniformly distributed in the interval
are i.i.d. integer random variables uniformly distributed in the interval  .
.
3.2. C-Lpcd
An important limitation of the LPCD model is the lack of memory. This is likely to be a problem from a perceptual point of view: with no constraints on the smoothness of the displacement field, there is no guarantee that the set of LPCD distortions is perceptually admissible even by considering very small values of  .
.
One way to overcome the limitation of the LPCD model, and to obtain better results from a perceptual point of view, is to require that the sample order, in the 1D case, is preserved (thus introducing memory in the system). In practice, the displacement of each element  of the distorted sequence
of the distorted sequence  is conditioned on the displacement of the element
is conditioned on the displacement of the element  of the same sequence. In formulas,
of the same sequence. In formulas,  , where
, where  is a sequence of i.i.d integer random variables uniformly distributed in the interval
is a sequence of i.i.d integer random variables uniformly distributed in the interval  . In the sequel, we will refer to this new class of DAs as C-LPCD (constrained local permutation with cancelation and duplication). Figure 1 illustrates the behavior of the C-LPCD model in the 1D case with
. In the sequel, we will refer to this new class of DAs as C-LPCD (constrained local permutation with cancelation and duplication). Figure 1 illustrates the behavior of the C-LPCD model in the 1D case with  . We know that
. We know that  , let us assume that
, let us assume that  is chosen in the interval
is chosen in the interval  (the solid-line box) and that
(the solid-line box) and that  , it means that
, it means that  . At the next step, we know that
. At the next step, we know that  , where
, where  , due to the position of the pixel
, due to the position of the pixel  , must be chosen in the interval
, must be chosen in the interval  (the bold dotted-line box). The interval
(the bold dotted-line box). The interval  is smaller than
is smaller than  because the position of the element
because the position of the element  cannot precede that of the element
cannot precede that of the element  . For example,
. For example,  could be equal to
could be equal to  yielding
yielding  .
.
The C-LPCD model can be mathematically described by resorting to the theory of Markov chains. For simplicity, let us focus again on the one-dimensional case. It is possible to design a Markov chain whose states correspond to the possible sizes of the interval  .
.
In a general case, given  , the maximum size of
, the maximum size of  is equal to
is equal to  (the minimum being equal to 2) and the transition matrix of the Markov chain (whose size is
(the minimum being equal to 2) and the transition matrix of the Markov chain (whose size is  ) is
) is

where each element  of the matrix is the transition probability of going from state
of the matrix is the transition probability of going from state  to state
to state  .
.
A visual inspection conducted on a set of images distorted with the C-LPCD model reveals that changing the value of  does not change the perceived intensity of the deformation.
does not change the perceived intensity of the deformation.
This effect, which can be described by resorting to the properties of Markov chains [12], can be avoided by allowing the model to generate a larger variety of displacement fields. For this reason, we modified the Markov chain by changing the transition probabilities among the states in order to give a greater probability to the transitions that result in a larger interval  . A way to do this is to assign the same probability (equal to
. A way to do this is to assign the same probability (equal to  ) to the transitions that cause a decrease of the size of
) to the transitions that cause a decrease of the size of  , corresponding to the elements
, corresponding to the elements  with
with  and
and  of the transition matrix, and to assign all the remaining probability mass, equal to
of the transition matrix, and to assign all the remaining probability mass, equal to  , to the transition corresponding to the element
, to the transition corresponding to the element  with
with  and
and  , that is, the transition whose effect is to enlarge the interval
, that is, the transition whose effect is to enlarge the interval  . The corresponding transition matrix becomes
. The corresponding transition matrix becomes

Figure 2 shows the limit probability distribution of the states versus  for the described Markov chain.
for the described Markov chain.
By looking at the figure, it is possible to note that regardless of the value of  , all the states have almost the same limit probabilities.
, all the states have almost the same limit probabilities.
The extension of the C-LPCD model to the 2D case is obtained by applying the 1D algorithm by rows to obtain the horizontal displacement field  , and by columns for the vertical displacements
, and by columns for the vertical displacements  .
.
3.3. Multiresolution Extension
To make the distortion less perceptible, we considered a multiresolution version of the LPCD and C-LPCD attacks, whereby the DAs are applied at different resolutions to obtain the global displacement field: a low-resolution displacement field is first generated, then a full-size displacement is built by means of a bicubic interpolation. The full resolution field is applied to the original image to produce the distorted image.
More specifically, the multiresolution models consist of two steps. Let  be the size of the image (for sake of simplicity, we assume that
be the size of the image (for sake of simplicity, we assume that  is a power of 2). To apply the LPCD (or C-LPCD) model at the
is a power of 2). To apply the LPCD (or C-LPCD) model at the  th level of resolution, two displacement fields
th level of resolution, two displacement fields  and
and  with size
with size  are generated. Then, the full-resolution fields
are generated. Then, the full-resolution fields  and
and  are built by means of bicubic interpolation. Note that this way noninteger displacement values are introduced. It is still possible to obtain integer displacements by applying a nearest neighbor interpolation instead of a bicubic one (of course at the expense of the smoothness of the displacement field). The full-resolution displacement fields
are built by means of bicubic interpolation. Note that this way noninteger displacement values are introduced. It is still possible to obtain integer displacements by applying a nearest neighbor interpolation instead of a bicubic one (of course at the expense of the smoothness of the displacement field). The full-resolution displacement fields  and
and  are used to generate the warped image
are used to generate the warped image  as follows:
as follows:

As opposed to the original version of LPCD and C-LPCD, however, the presence of noninteger displacements is now possible due to the interpolation. To account for this possibility, whenever the displacement vector points to noninteger coordinates of the original image, the gray level of the attacked image  is computed by means of the bicubic interpolation. While the above interpolation does not have a significant impact on the visual quality of the attacked image, the possible introduction of new gray levels, which were not present in the original image, complicates the LPCD and C-LPCD models, by making it more difficult to describe the attacked signal as a hidden Markov process (as we did in Section 3.1).
is computed by means of the bicubic interpolation. While the above interpolation does not have a significant impact on the visual quality of the attacked image, the possible introduction of new gray levels, which were not present in the original image, complicates the LPCD and C-LPCD models, by making it more difficult to describe the attacked signal as a hidden Markov process (as we did in Section 3.1).
The pseudocode description of the multiresolution version of LPCD DAs is provided by Algorithms 1 and 2.
3.4. Cardinality Evaluation
A measure of the difficulty of coping with a given type of DA is given by the cardinality of the attack class. In fact, the larger is the DA space, the more difficult will be to recover the synchronization between the embedded and the detector, both in terms of complexity and accuracy. As a matter of fact, it is possible to show [3, 11] that as long as the cardinality of the DAs is subexponential, the exhaustive search of the watermark results in asymptotically optimum watermark detection with no loss of accuracy with regard to false-detection probability. By contrast, when the size of the DA is exponential, simply considering all the possible distortions may not be a feasible solution both from the point of view of computational complexity and detection accuracy [11]. In order to evaluate the cardinality of the classes of DAs, the perceptual impact of LPCD and C-LPCD must be taken into account. Thus, we first found the limits of the model parameters by means of perceptual considerations, then we estimated the cardinality of the various classes of LPCD DAs.
Let us observe that from a perceptual point of view, LPCD DAs have a different behavior for different values of  and for different levels of resolution
and for different levels of resolution  , in particular, the image quality increases if the attacks are applied to a lower level of resolution (larger
, in particular, the image quality increases if the attacks are applied to a lower level of resolution (larger  ) but, at the same time, the number of possible distortions decreases.
) but, at the same time, the number of possible distortions decreases.
In a previous work [13], both subjective and objective tests were performed to establish the sensitivity of the human visual system to the geometric distortions introduced by the LPCD model as a function of the control parameters  and
and  . This way, the authors were able to identify the range of values of the control parameters that do not affect image quality: for each level of resolution, the maximum value of
. This way, the authors were able to identify the range of values of the control parameters that do not affect image quality: for each level of resolution, the maximum value of  that can be used while keeping the distortion invisible was found. For instance, in the case of images of size
that can be used while keeping the distortion invisible was found. For instance, in the case of images of size  , the maximum admissible geometric distortions are obtained by using
, the maximum admissible geometric distortions are obtained by using  for the LPCD model and
for the LPCD model and  ,
,  or
or  for the C-LPCD model (for higher level of resolution, it is not possible to find an adequate value of
for the C-LPCD model (for higher level of resolution, it is not possible to find an adequate value of  resulting in an invisible distortion).
resulting in an invisible distortion).
In Figure 3, two examples of displacement fields generated with the LPCD attack with  and
and  Figure 3(a) and the C-LPCD attack with
Figure 3(a) and the C-LPCD attack with  and
and  Figure 3(b) are given: as expected, by applying the model to a lower level of resolution, it is possible to obtain a more uniform field (for the purpose of visibility, the total displacement field is cropped and only one vector every sixteen samples is depicted in the figure).
Figure 3(b) are given: as expected, by applying the model to a lower level of resolution, it is possible to obtain a more uniform field (for the purpose of visibility, the total displacement field is cropped and only one vector every sixteen samples is depicted in the figure).
We can now use the above considerations to estimate the cardinality of the class of LPCD DAs. For the LPCD model, the number of possible admissible geometric distortions is simply equal, neglecting the boundary effects, to  , where
, where  is the size of the image. Then, if we consider a
is the size of the image. Then, if we consider a  image, and if we take into account the perceptual analysis in [13], then we obtain
image, and if we take into account the perceptual analysis in [13], then we obtain  different attacked images.
different attacked images.
With regard to the C-LPCD model, we need to refer again to the theory of Markov chains. Let us consider the one-dimensional case and the graph of the Markov chain describing the C-LPCD model. It is possible to construct the adjacency matrix  of zeroes and ones, where
of zeroes and ones, where  if in the graph there is an edge going from node
if in the graph there is an edge going from node  to node
to node  and zero, otherwise. The number of paths of length
and zero, otherwise. The number of paths of length  that start from node
that start from node  and end into node
and end into node  is given by the
is given by the  entry of the matrix
entry of the matrix  . The exponential growth rate of the number of paths of length
. The exponential growth rate of the number of paths of length  in the graph is
in the graph is  , where
, where  is the largest eigenvalue of A. In the C-LPCD case, the practical values of
is the largest eigenvalue of A. In the C-LPCD case, the practical values of  are not very large, for instance, for a 512
are not very large, for instance, for a 512  512 image, with
512 image, with  , we have
, we have  , then we can easily compute the matrix
, then we can easily compute the matrix  and derive the exact size of the C-LPCD class of attacks. Specifically, by remembering that the two-dimensional extension of C-LPCD is obtained by applying the one-dimensional C-LPCD DA first by rows and then by columns, we obtain the results reported in Table 1.
and derive the exact size of the C-LPCD class of attacks. Specifically, by remembering that the two-dimensional extension of C-LPCD is obtained by applying the one-dimensional C-LPCD DA first by rows and then by columns, we obtain the results reported in Table 1.
With the above approach, we were able to count all the distortions that can be generated with the C-LPCD model. Nevertheless, as explained in the previous subsection, the occurrence of a particular distortion configuration depends on the Markov chain-transition matrix and is not constant for all the configurations. Thus, for a more appropriate evaluation of the cardinality of C-LPCD DAs, we need to refer to the entropy rate of the corresponding Markov chain. In this context, the following result from information theory [14] is useful: let  be a stationary Markov chain with stationary distribution
be a stationary Markov chain with stationary distribution  and transition matrix
and transition matrix  , then the entropy rate is
, then the entropy rate is

The knowledge of the entropy rate of the Markov chain and the asymptotic equipartition property (AEP) [14] help us to find the number of possible distortions that can be generated with a so-defined Markov chain, since it asymptotically corresponds to the number of typical sequences, that is,  . After some algebraic manipulations, we find that in the case of C-LPCD with
. After some algebraic manipulations, we find that in the case of C-LPCD with  and
and  ,
,  is approximately equal to
is approximately equal to  bits and the number of different distortions that is possible to generate is
bits and the number of different distortions that is possible to generate is  . In the same way, in the case of C-LPCD with
. In the same way, in the case of C-LPCD with  and
and  , it is possible to generate
, it is possible to generate  different distortions. By looking at Table 1, we can see that, as we expected, the cardinality of C-LPCD evaluated by considering the entropy rate of the Markov chain (second row) is much smaller than the number of possible distortions (first row). We conclude this section by observing that the size of both the LPCD and the C-LPCD DAs exhibit an exponential growth, with the constrained model resulting in a higher growth rate. For this reason, both classes of attacks are likely to make watermark detection rather difficult, and will need to be carefully considered in future works on DA-resistent watermarking.
different distortions. By looking at Table 1, we can see that, as we expected, the cardinality of C-LPCD evaluated by considering the entropy rate of the Markov chain (second row) is much smaller than the number of possible distortions (first row). We conclude this section by observing that the size of both the LPCD and the C-LPCD DAs exhibit an exponential growth, with the constrained model resulting in a higher growth rate. For this reason, both classes of attacks are likely to make watermark detection rather difficult, and will need to be carefully considered in future works on DA-resistent watermarking.
4. Markov Field Da (mf-Da)
One problem with the C-LPCD attack is that it does not take into account the two-dimensional nature of images since it is based on a one-dimensional Markov chain. To overcome this limitation, we introduce a new class of DAs based on the theory of Markov random fields. We will refer to this new class of attacks as MF-DA.
Markov random field theory is a branch of probability theory for analyzing the spatial or contextual dependencies of physical phenomena. The foundations of the theory of Markov random fields may be found in statistical physics of magnetic materials (Ising models, spin glasses, etc.) and also in solids and crystals, where the molecules are arranged in a lattice structure and there are interactions with close neighbors (e.g., Debye's theory for the vibration of atoms in a lattice is based on a model of quantum harmonic oscillators with coupling among nearest neighbors). Markov random fields are often used in image processing applications, because this approach defines a model for describing the correlation among neighboring pixels [15].
4.1. Model Description
Many vision problems can be posed as labeling problems in which the solution of a problem is a set of labels assigned to image pixels or features. A labeling problem is specified in terms of a set of sites and a set of labels. Let  be a discrete set of
be a discrete set of  sites in which
sites in which  are indices (a site often represents a point or a region in the Euclidean space such as an image pixel or an image feature). A label is an event that may happen to a site. Let
are indices (a site often represents a point or a region in the Euclidean space such as an image pixel or an image feature). A label is an event that may happen to a site. Let  be a set of labels. The labeling problem is to assign a label from
be a set of labels. The labeling problem is to assign a label from  to each of the sites in
to each of the sites in  . In the terminology of random fields, a labeling is called a configuration.
. In the terminology of random fields, a labeling is called a configuration.
The sites in  are related to one another via a neighborhood system. A neighborhood system for
are related to one another via a neighborhood system. A neighborhood system for  is defined as
is defined as  , where
, where  is the set of sites neighboring
is the set of sites neighboring  . The neighboring relationship has the following properties:
. The neighboring relationship has the following properties:
-
(1)
a site is not neighboring to itself:
 ,
, -
(2)
the neighboring relationship is mutual:
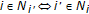 .
.
If  is a regular lattice, the neighboring set of
is a regular lattice, the neighboring set of  is often defined as the set of nearby sites within a radius of
is often defined as the set of nearby sites within a radius of  :
:

Once introduced a set  and a neighborhood system
and a neighborhood system  , it is possible to define a clique
, it is possible to define a clique  for
for  like a subset of sites in
like a subset of sites in  . It consists either of a single-site
. It consists either of a single-site  (single-site clique), or a pair of neighboring sites
(single-site clique), or a pair of neighboring sites  (pair-sites cliques), or a triple of neighboring sites
(pair-sites cliques), or a triple of neighboring sites  (triple-sites cliques), and so on.
(triple-sites cliques), and so on.
The collections of single-site, pair-site, and triple-site, cliques will be denoted by  ,
,  , and
, and  , respectively, where
, respectively, where

The collection of all cliques for  is denoted by
is denoted by  .
.
Figure 4 shows a first-order neighborhood system, also called a  -neighborhood system, with the four corresponding pair-sites cliques. The
-neighborhood system, with the four corresponding pair-sites cliques. The  symbol denotes the considered site and the letters indicate its neighbors.
symbol denotes the considered site and the letters indicate its neighbors.
A random field  is a family of random variables defined on a set
is a family of random variables defined on a set  , in which each random variable
, in which each random variable  takes a value
takes a value  in a set of labels
in a set of labels  .
.
 is said to be a Markov random field (MRF) on
is said to be a Markov random field (MRF) on  with respect to a neighborhood system
with respect to a neighborhood system  if and only if the two following conditions are satisfied:
if and only if the two following conditions are satisfied:

where  is a configuration of
is a configuration of  (corresponding to a realization of the field),
(corresponding to a realization of the field),  is the joint probability
is the joint probability  of the joint event
of the joint event  , that is, it measures the probability of the occurrence of a particular configuration, and
, that is, it measures the probability of the occurrence of a particular configuration, and

denotes the set of values at the sites neighboring  , that is, the neighborhood
, that is, the neighborhood  centered at position
centered at position  . The positivity is due to technical reasons, since it is a necessary condition if we want the Hammersley-Clifford theorem (see below) to hold [16].
. The positivity is due to technical reasons, since it is a necessary condition if we want the Hammersley-Clifford theorem (see below) to hold [16].
To exploit MRFs characteristics in a practical way, we need to refer to the Hammersley-Clifford theorem [15] for which  is an MRF on
is an MRF on  with respect to
with respect to  if and only if
if and only if  is a Gibbs random field (GRF) on
is a Gibbs random field (GRF) on  with respect to
with respect to  , that is, the probability distribution of an MRF has the form of a Gibbs distribution:
, that is, the probability distribution of an MRF has the form of a Gibbs distribution:

where  is a normalizing constant called the partition function,
is a normalizing constant called the partition function,  is a constant called the temperature, and
is a constant called the temperature, and  is the energy function. The energy function
is the energy function. The energy function

is a sum of cliques potentials,  , over all possible cliques
, over all possible cliques  . Thus the value of
. Thus the value of  depends on the local configuration on the clique
depends on the local configuration on the clique  . The practical value of the theorem is that it provides a simple way of specifying the joint probability. Since
. The practical value of the theorem is that it provides a simple way of specifying the joint probability. Since  measures the probability of the occurrence of a particular configuration, we know that the more probable configurations are those with lower energies.
measures the probability of the occurrence of a particular configuration, we know that the more probable configurations are those with lower energies.
In our case, we can model geometric attacks with a random field  defined on the set
defined on the set  of the image pixels. The value assumed by each random variable represents the displacement associated to a particular pixel. Specifically, for each pixel, we have two values for the two directions
of the image pixels. The value assumed by each random variable represents the displacement associated to a particular pixel. Specifically, for each pixel, we have two values for the two directions  and
and  . For this reason, each variable
. For this reason, each variable  is assigned a displacement vector
is assigned a displacement vector  . The advantage brought by MRF theory is that by letting the displacement field of a generic point
. The advantage brought by MRF theory is that by letting the displacement field of a generic point  of the image depend on the displacement fields of the other points of its neighborhood (let us indicate this set with the notation
of the image depend on the displacement fields of the other points of its neighborhood (let us indicate this set with the notation  ), we can automatically impose that the resulting displacement field is smooth enough to avoid annoying geometrical distortions.
), we can automatically impose that the resulting displacement field is smooth enough to avoid annoying geometrical distortions.
As we said, an MRF is uniquely determined once the Gibbs distribution and the neighborhood system are defined. In the approach proposed here, for each pixel  , only four neighbors of first order and the corresponding four pair-site cliques, as described by Figure 4. The potential function we used is a bivariate normal distribution expressed by:
, only four neighbors of first order and the corresponding four pair-site cliques, as described by Figure 4. The potential function we used is a bivariate normal distribution expressed by:

where  and
and  are the components of the displacement vector
are the components of the displacement vector  associated to the pixel
associated to the pixel  ,
,  is a point belonging to the 4-neighborhood of
is a point belonging to the 4-neighborhood of  ,
,  and
and  are the x,y components of the displacement vector
are the x,y components of the displacement vector  associated to the pixel
associated to the pixel  and
and  and
and  are the two components of the standard deviation vector
are the two components of the standard deviation vector  (these values are controlled by perceptual constraints).
(these values are controlled by perceptual constraints).
A typical application of MRF in the image processing field is to recover the original version of an image (or a motion vector field) by relying on a noisy version of the image. By assuming that the original image can be described by means of an MRF, the above problem is formulated as a maximum a posteriori estimation problem. Thanks to the Hammersley-Clifford theorem, this corresponds to an energy minimization problem that is usually solved by applying an iterative relaxation algorithm to the noisy version of the image [16]. The problem we have to face here, however, is slightly different. We simply want to generate a displacement field according to the Gibbs probability distribution defined by (16) and the particular potential function expressed in (18).
To do so, the displacement field is initialized by assigning to each pixel  in the image a displacement vector
in the image a displacement vector  generated randomly (and independently on the other pixels) in the interval in
generated randomly (and independently on the other pixels) in the interval in  with
with  (the value of
(the value of  is determined by relying on perceptual considerations). This initial random field is treated as a noisy version of an underlying displacement field obeying the MF-DA model. The MF-DA field is then obtained by applying an iterative smoothing algorithm to the randomly generated field. More specifically, the technique we used visits all the points of the displacement field and updates their values through the iterated conditional mode (ICM) algorithm detailed in [16]. Specifically, when the ICM algorithm starts, all the pixels
is determined by relying on perceptual considerations). This initial random field is treated as a noisy version of an underlying displacement field obeying the MF-DA model. The MF-DA field is then obtained by applying an iterative smoothing algorithm to the randomly generated field. More specifically, the technique we used visits all the points of the displacement field and updates their values through the iterated conditional mode (ICM) algorithm detailed in [16]. Specifically, when the ICM algorithm starts, all the pixels  of the displacement field are randomly visited and their displacement vectors updated by trying to minimize the potential function (18). Specifically, a local minimum is sought by letting
of the displacement field are randomly visited and their displacement vectors updated by trying to minimize the potential function (18). Specifically, a local minimum is sought by letting

Note that in the above equation, the displacements of the pixels in the neighborhood of  are fixed, hence resulting in a local minimization of the Gibbs potential. After each pixel is visited and the corresponding displacement gets updated, a new iteration starts. The algorithm ends when no new modification is introduced for a whole iteration, which is usually the case after 7-8 iterations.
are fixed, hence resulting in a local minimization of the Gibbs potential. After each pixel is visited and the corresponding displacement gets updated, a new iteration starts. The algorithm ends when no new modification is introduced for a whole iteration, which is usually the case after 7-8 iterations.
As for the LPCD DAs, we considered a multiresolution version of the MF-DA, where the full-resolution version of the the displacement field is built by interpolating the displacement field obtained by applying the MF-DA at a resolution level  . In Figures 5(a) and 5(b), two examples of displacement fields generated with the MF-DA model are shown, using respectively, the parameters
. In Figures 5(a) and 5(b), two examples of displacement fields generated with the MF-DA model are shown, using respectively, the parameters  and
and  . With MF-DA, it is possible to obtain larger displacement vectors than with the LPCD attacks (due to the high value of the
. With MF-DA, it is possible to obtain larger displacement vectors than with the LPCD attacks (due to the high value of the  parameter), while keeping the distortion invisible, thanks to the ability of the iterative conditional mode to generate a very smooth field, as we can see from Figure 5. A pseudocode description of the MF-DA is provided by Algorithms 3, 4, and 5.
parameter), while keeping the distortion invisible, thanks to the ability of the iterative conditional mode to generate a very smooth field, as we can see from Figure 5. A pseudocode description of the MF-DA is provided by Algorithms 3, 4, and 5.
4.2. Perceptual Analysis
In order to evaluate the potentiality of the MF-DA class of attacks, the perceptual impact of the distortion they generate must be taken into account. From a perceptual point of view, MRF DAs have a different behavior for different values of  ,
,  , and
, and  , in particular, the image quality increases if the attacks are generated at a lower level of resolution but, in the meantime, the number of possible distortions decreases.
, in particular, the image quality increases if the attacks are generated at a lower level of resolution but, in the meantime, the number of possible distortions decreases.
After a visual inspection conducted on a set of images, we found, for each level of resolution, the maximum value of the  components and
components and  that can be used while keeping the distortion invisible. Specifically, we found that, in case of images of size
that can be used while keeping the distortion invisible. Specifically, we found that, in case of images of size  , the larger perceptually admissible displacements are obtained by using
, the larger perceptually admissible displacements are obtained by using  and
and  .
.
In Figure 6, two examples of images distorted with an MF-DA attack applied at different levels of resolution are shown: in the Barbara image, the MRF is applied at a lower level of resolution (  ), while in the Lena image, the distortion is generated at a higher level of resolution
), while in the Lena image, the distortion is generated at a higher level of resolution  . In both cases by comparing the original image (on the left) with the attacked one (on the right), we can notice a slightly perceptible distortion that is, however, not annoying due to the smoothness constraints of the field (the distortion is not visible if only the attacked image is provided so that the comparison with the original image is not possible).
. In both cases by comparing the original image (on the left) with the attacked one (on the right), we can notice a slightly perceptible distortion that is, however, not annoying due to the smoothness constraints of the field (the distortion is not visible if only the attacked image is provided so that the comparison with the original image is not possible).
Regarding the cardinality evaluation of this new class of DAs, in principle all the displacement fields are allowed, with the most annoying distortions corresponding to very low probabilities (and thus very large Gibbs potential). In order to evaluate the cardinality of the MF-DA class, then, a first step would be to calculate the entropy rate of the field. However, this is a prohibitive task given that no technique is known to calculate the entropy rate of even the simplest MRFs.
5. Desynchronization Properties of The Various Das
In this section, we evaluate the desynchronization capability of the various classes of attacks. To do so, two very simple watermarking algorithms were implemented and the ability of the various DAs to inhibit watermark detection was evaluated. The source image database used for the experiments includes the six standard images: Baboon, Barbara, Boats, Goldhill, Lena, and Peppers. The source image database and the software we used for the experiments are available on http://www.dii.unisi.it/~vipp.
The tested algorithms include
-
(i)
blind additive spread spectrum in the frequency domain (BSS-F),
-
(ii)
blind additive spread spectrum in the wavelet domain (BSS-W).
In both the systems, the watermark consists of a sequence of  bits
bits  ; each value
; each value  being a random scalar that is either
being a random scalar that is either  or
or  with equal probability.
with equal probability.
In the BSS-F algorithm, the watermark is inserted into the middle frequency coefficients of the full-frame DCT domain. The DCT of the original image is computed, the frequency coefficients are reordered in a zig-zag scan, and the first  coefficients are selected to generate a vector
coefficients are selected to generate a vector  . Then, in order to obtain a tradeoff between perceptual invisibility and robustness to image processing techniques, the lowest
. Then, in order to obtain a tradeoff between perceptual invisibility and robustness to image processing techniques, the lowest  coefficients are skipped and the watermark
coefficients are skipped and the watermark  is embedded in the last
is embedded in the last  coefficients
coefficients  to obtain a new vector
to obtain a new vector  according to the following rule:
according to the following rule:

where  is the embedding strength and PN is a uniformly distributed pseudorandom sequence of
is the embedding strength and PN is a uniformly distributed pseudorandom sequence of  and
and  . (20) refers to the embedding of one bit, the extension to multiple bits consists of applying (20) for each bit considering each time a different subset of 0
. (20) refers to the embedding of one bit, the extension to multiple bits consists of applying (20) for each bit considering each time a different subset of 0  and a different PN sequence (a more-detailed description of the watermark embedding is given by the Algorithm 4).
and a different PN sequence (a more-detailed description of the watermark embedding is given by the Algorithm 4).
In watermark detection, the DCT is applied to the watermarked (and possibly attacked) image, the DCT coefficients are reordered into a zig-zag scan, and the coefficients from the  th to the
th to the  are selected to generate a vector
are selected to generate a vector  . For each bit, the correlation coefficient between the corresponding subset of the
. For each bit, the correlation coefficient between the corresponding subset of the  vector and a new PN sequence is evaluated and compared to a threshold (equal to
vector and a new PN sequence is evaluated and compared to a threshold (equal to  ) to recover the embedded bit.
) to recover the embedded bit.
The correlation coefficient is evaluated in the following way:

where  and
and  are two vectors of same size
are two vectors of same size  and
and  is the mean operator. The decision rule states that,
is the mean operator. The decision rule states that,

In the BSS-W watermarking system, the watermark is added to the DWT coefficients of the three largest detail (i.e., LH, HL, HH) subbands of the image. The embedding and decoding functions are implemented in the same way of the previous system but the watermark is inserted in the wavelet coefficients obtained with a one-step wavelet decomposition. A more-detailed description of the two watermarking systems is given by the Algorithms 6, 7, 8, and 9.
The six standard images were watermarked with the systems described above with different payloads and then attacked with RBA and the two new classes of attacks. Each image is attacked with a different realization of the field. In Table 2, the values of the parameters used for the experiments are shown. Figures 7 and 8 show the ability of the RBA and of the two new DAs to inhibit correct decoding. The average of the bit-error rate obtained for the six images is plotted versus different values of the payload for both the watermarking systems.
For both the systems, the RBA attack is not able to prevent a correct watermark decoding, in fact, the RBA plot is not visible in the figures because the bit-error rate is always equal to zero. A more powerful class of DAs is the LPCD DAs that in both the systems gives a bit-error rate much higher than the RBA attack. The MF-DA always results in a very high bit-error rate also applying the attack to a lower level of resolution.
6. Conclusion
In this paper, we introduced two new classes of desynchronization attacks that extend the class of local geometric attacks so to allow for more powerful attacks with respect to classical RBA. The effectiveness of the new classes of DAs is evaluated from different perspectives including perceptual intrusiveness and desynchronization efficacy. The experimental results showed that the two new classes of attacks are more powerful than the local geometric attacks proposed so far.
This work can be seen as a first step towards the characterization of the whole class of perceptually admissible DAs, which in turn is an essential step towards the development of a new class of watermarking systems that can effectively cope with them.
Future works may include the development of a perceptual metric suited for geometric distortions and the use of new potential functions.
Algorithm 1: LPCD model.
-
1.
Read image to be attacked Y, read size of the window
 , read level of resolution
, read level of resolution 
-
2.
 size of the low resolution displacement field
size of the low resolution displacement field
-
3.
Initialize matrices
 and
and  of horizontal and vertical displacement fields to
of horizontal and vertical displacement fields to 
-
4.
for
 do
do
-
5.
for
 do
do
-
6.
If
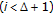 or
or  then
then -
7.
 and
and  are randomly chosen in
are randomly chosen in 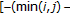


-
8.
else if
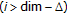 or
or 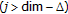 then
then -
9.
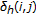 and
and  are randomly chosen in
are randomly chosen in 


-
10.
else
-
11.
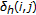 and
and  are randomly chosen in
are randomly chosen in 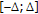
-
12.
end if
-
13.
end for
-
14.
end for
-
15.
Resize the displacement fields given by
 and
and  to the image size through
to the image size through
 bicubic interpolation provided by the matlab function
bicubic interpolation provided by the matlab function 
 to obtain
to obtain
 the high resolution displacement fields
the high resolution displacement fields  an
an 
-
16.
for
 do
do
-
17.
for
 do
do
-
18.
 Apply the displacement fields
Apply the displacement fields
 to the image, to obtain the attacked image Z, by means of bicubic
to the image, to obtain the attacked image Z, by means of bicubic
 interpolation
interpolation
-
19.
end for
-
20.
end for
Algorithm 2: Constrained LPCD model (modified version).
-
1.
Read image to be attacked, read size of the window
 , read level of resolution
, read level of resolution 
-
2.

 size of the low resolution displacement field
size of the low resolution displacement field
-
3.
Initialize matrices
 and
and 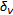 of horizontal and vertical displacement fields to
of horizontal and vertical displacement fields to 
-
4.
for
 do
do
-
5.
for
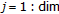 do
do
-
6.
if
 or
or  then
then -
7.
 and
and 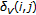 are randomly chosen in
are randomly chosen in 


-
8.
else if
 or
or  Then
Then -
9.
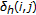 and
and  are randomly chosen in
are randomly chosen in 


-
10.
else
-
11.
 is chosen in
is chosen in 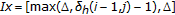 with a
with a
 distribution vector
distribution vector 
-
12.
 is chosen in
is chosen in 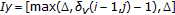 with a
with a
 distribution vector
distribution vector 
-
13.
end if
-
14.
end for
-
15.
end for
-
16.
Resize the displacement fields given by
 and
and 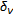 to the image size through
to the image size through
 bicubic interpolation provided by the matlab function
bicubic interpolation provided by the matlab function  to obtain
to obtain
 the high resolution displacement fields
the high resolution displacement fields  an
an 
-
17.
for
 do
do
-
18.
for
 do
do
-
19.
 Apply the displacement fields
Apply the displacement fields
 to the image, to obtain the attacked image Z, by means of bicubic
to the image, to obtain the attacked image Z, by means of bicubic
 interpolation
interpolation
-
20.
end for
-
21.
end for
Algorithm 3: MF-DA-based model.
-
1.
Read image to be attacked, read level of resolution
 , read standard deviation
, read standard deviation  , read
, read 
-
2.
 size of the low resolution displacement fields
size of the low resolution displacement fields 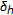 and
and 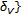
-
3.
Initialize matrices
 and
and 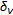 with random values in the interval
with random values in the interval 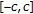
-
4.
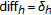
-
5.
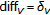
-
6.
while
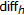 and
and  are
are  do
do -
7.
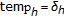
-
8.

-
9.
row = randperm(dim);
-
10.
col = randperm(dim);
-
11.
for
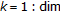 do
do
-
12.
for
 do
do
-
13.
i = col(1, k);
-
14.
j = row(1, h)
-
15.
 Find the optimum
Find the optimum
 displacements
displacements  and
and  , i.e. the ones minimizing the potential
, i.e. the ones minimizing the potential
 function
function
-
16.
-
17.
-
18.
end for
-
19.
end for
-
20.

-
21.

-
22.
end while
-
23.
Resize the displacement fields given by
 and
and  to the image size through
to the image size through
 bicubic interpolation provided by the matlab function
bicubic interpolation provided by the matlab function  to obtain
to obtain
 the high resolution displacement fields
the high resolution displacement fields  an
an 
-
24.
for
 do
do
-
25.
for
 do
do
-
26.
 Apply the displacement fields
Apply the displacement fields
 to the image, to obtain the attacked image Z, by means of bicubic
to the image, to obtain the attacked image Z, by means of bicubic
 interpolat
interpolat
-
27.
end for
-
28.
end for
Algorithm 4: Function  .
.
-
1.
Read position of the pixel
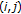 , matrices of displacement fields
, matrices of displacement fields 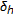 and
and  ,
,
 standard deviation
standard deviation 
-
2.
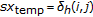
-
3.

-
4.
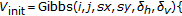 Initial potential
Initial potential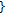
-
5.
for
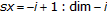 do
do
-
6.
for
 do
do
-
7.
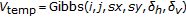
-
8.
if
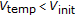 then
then
-
9.

-
10.
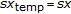
-
11.
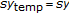
-
12.
end if
-
13.
end for
-
14.
end for
-
15.

-
16.
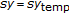
-
17.
return
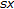 and
and 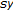
Algorithm 5: Potential funtion  .
.
-
1.
Read position of the pixel
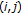 , displacements
, displacements 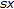 and
and 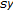 , matrices of
, matrices of
 displacement fields
displacement fields  and
and 
-
2.

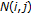 is a first order
is a first order
 neighborhood system associated with the pixel
neighborhood system associated with the pixel 
-
3.
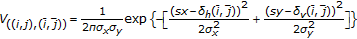
-
4.
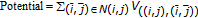
-
5.
return Potential
Algorithm 6: DCT domain watermarking: embedding.
-
1.
Read image to be watermarked, length of the watermark
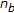 , energy of the
, energy of the
 watermark
watermark  , seed
, seed 
-
2.
Generate a random
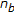 long message
long message -
3.
Perform full-frame DCT
-
4.
Reorder the DCT coefficients into a zig-zag scan
-
5.
Select the coefficients:
 middle
middle
 frequency coefficients to be watermarked
frequency coefficients to be watermarked
-
6.
for bit = 1:
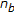 do
do -
7.
Generate an antipodal PN sequence of length
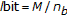
-
8.
 and
and 
-
9.
if bit = 0 then
-
10.
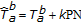
-
11.
else
-
12.

-
13.
end if
-
14.
end for
-
15.
Reinsert the vector
 in the zig-zag scan
in the zig-zag scan -
16.
Perform inverse scan
-
17.
Perform inverse full frame DCT
-
18.
Save watermarked image and message
Algorithm 7: DCT domain watermarking: decoding.
-
1.
Read watermarked image, seed key, length of the watermark
 and load
and load
 inserted message
inserted message  needed to evaluate bit error rat
needed to evaluate bit error rat
-
2.
Perform full frame DCT transform
-
3.
Reorder the DCT coefficients into a zig-zag scan
-
4.
Select the coefficients:
 middle
middle
 frequency watermarked coefficients
frequency watermarked coefficients
-
5.
for bit = 1:
 do
do -
6.
Generate an antipodal PN sequence of length
-
7.
Compute the correlation coefficient as expressed in (21) between
 PN and
PN and  where
where  and
and 
-
8.
end for
-
9.
for bit = 1:
 do
do -
10.
if correlation(bit) > 0 Then
-
11.
extracted_message(bit) = 0
-
12.
else
-
13.
extracted_message(bit) = 1
-
14.
end if
-
15.
end for
-
16.
return Bit Error Rate
Algorithm 8: DWT domain watermarking: embedding.
-
1.
Read image to be watermarked, length of the watermark
 , energy of the
, energy of the
 watermark
watermark  , seed key
, seed key
-
2.
Generate a random
 long message
long message -
3.
Perform a one step wavelet decomposition using Haar filter
-
4.
Reorder the LH, HL and HH components into a vector

-
5.
for bit = 1:
 do
do -
6.
Generate an antipodal PN sequence of length
-
7.
 and
and 
-
8.
if bit = 0 then
-
9.

-
10.
else
-
11.
-
12.
end if
-
13.
end for
-
14.
Perform a one step inverse wavelet decomposition using Haar filter
-
15.
Save watermarked image and message
Algorithm 9: DWT domain watermarking: decoding.
-
1.
Read watermarked image, seed
 , length of the watermark
, length of the watermark 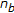 and load
and load
 inserted message
inserted message  needed to evaluate bit error rate
needed to evaluate bit error rate
-
2.
Perform a one step wavelet decomposition using Haar filter
-
3.
Reorder the LH, HL and HH components into a vector
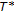
-
4.
for bit = 1:
 do
do -
5.
Generate an antipodal PN sequence of length

-
6.
Compute the correlation coefficient as expressed in (21) between
 PN and
PN and  where
where  and
and 
-
7.
end for
-
8.
for bit = 1:
 do
do -
9.
if correlation(bit) > 0 then
-
10.
extracted_message(bit) = 0
-
11.
else
-
12.
extracted_message(bit) = 1
-
13.
end if
-
14.
end for
-
15.
return Bit Error Rate
References
Petitcolas FAP: Stirmark benchmark 4.0. http://www.petitcolas.net/fabien/watermarking/stirmark
Lichtenauer J, Setyawan I, Kalker T, Lagendijk R: Exhaustive geometrical search and the false positive watermark detection probability. Security and Watermarking of Multimedia Contents V, January 2003, Santa Clara, Calif, USA, Proceedings of SPIE 5020: 203-214.
Barni M: Effectiveness of exhaustive search and template matching against watermark desynchronization. IEEE Signal Processing Letters 2005,12(2):158-161.
Voloshynovskiy S, Deguillaume F, Pun T: Multibit digital watermarking robust against local non linear geometrical distortions. Proceedings of IEEE International Conference on Image Processing (ICIP '01), October 2001, Thessaloniki, Greece 3: 999-1002.
Pereira S, Pun T: Fast robust template matching for affine resistant image watermarking. Proceedings of the 3rd International Workshop on Information Hiding (IH '99), September-October 1999, Dresden, Germany, Lecture Notes in Computer Science 1768: 199-210.
Pereira S, Ruanaidh JJKO, Deguillaume F, Csurka G, Pun T: Template based recovery of Fourier-based watermarks using log-polar and log-log maps. Proceedings of the 6th IEEE International Conference on Multimedia Computing and Systems (ICMCS '99), June 1999, Florence, Italy 1: 870-874.
Delannay D, Macq B: Generalized 2-D cyclic patterns for secret watermark generation. Proceedings of IEEE International Conference on Image Processing (ICIP '00), September 2000, Vancouver, BC, Canada 2: 72-79.
Kutter M: Watermarking resistance to translation, rotation, and scaling. Multimedia Systems and Applications, November 1998, Boston, Mass, USA, Proceedings of SPIE 3528: 423-431.
Lin C-Y, Wu M, Bloom JA, Cox IJ, Miller ML, Lui YM: Rotation, scale, and translation resilient watermaking for images. IEEE Transactions on Image Processing 2001,10(5):767-782. 10.1109/83.918569
Petitcolas FAP, Anderson RJ: Evaluation of copyright marking systems. Proceedings of the 6th IEEE International Conference on Multimedia Computing and Systems (ICMCS '99), June 1999, Florence, Italy 1: 574-579.
Merhav N: An information-theoretic view of watermark embedding-detection and geometric attacks. Proceedings of the 1st Wavila Challenge Workshop (WaCha '05), June 2005, Barcelona, Spain
Barni M, D'Angelo A, Merhav N: Expanding the class of watermak de-synchronization attacks. Proceedings of the 9th ACM Workshop on Multimedia and Security (MM-Sec '07), September 2007, Dallas, Tex, USA 195-204.
D'Angelo A, Menegaz G, Barni M: Perceptual quality evaluation of geometric distortions in images. Human Vision and Electronic Imaging XII, January 2007, San Jose, Calif, USA, Proceedings of SPIE 6492:-12.
Cover T, Thomas J: Elements of Information Theory. John Wiley & Sons, New York, NY, USA; 1991.
Li S: Markov Random Field Modeling in Computer Vision. Springer, London, UK; 1995.
Besag J: On the statistical analysis of dirty pictures. Journal of the Royal Statistical Society B 1986,48(3):259-302.
Acknowledgment
This work was supported by the Italian Ministry for University and Research, under FIRB Project no. RBIN04AC9W: "Image watermarking in the presence of geometric attacks, theoretical analysis, and development of practical algorithm."
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
D'Angelo, A., Barni, M. & Merhav, N. Stochastic Image Warping for Improved Watermark Desynchronization. EURASIP J. on Info. Security 2008, 345184 (2008). https://doi.org/10.1155/2008/345184
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/345184

 (one-dimensional case).
(one-dimensional case).

 .
.
 and
and  ; (b) C-LPCD with
; (b) C-LPCD with  and
and  .
. ,
,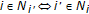 .
.

 ,
,  and
and  ; (b) MRF with
; (b) MRF with  ,
,  and
and  .
.
 ; (c) original image; (d) attacked image with
; (c) original image; (d) attacked image with  .
.

 , read level of resolution
, read level of resolution 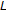
 size of the low resolution displacement field
size of the low resolution displacement field
 and
and  of horizontal and vertical displacement fields to
of horizontal and vertical displacement fields to 
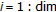 do
do
 do
do
 or
or  then
then and
and  are randomly chosen in
are randomly chosen in 
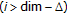 or
or 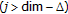 then
then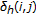 and
and  are randomly chosen in
are randomly chosen in 
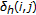 and
and  are randomly chosen in
are randomly chosen in 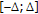
 and
and  to the image size through
to the image size through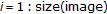 do
do
 do
do
 Apply the displacement fields
Apply the displacement fields , read level of resolution
, read level of resolution 

 size of the low resolution displacement field
size of the low resolution displacement field
 and
and 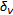 of horizontal and vertical displacement fields to
of horizontal and vertical displacement fields to 
 do
do
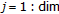 do
do
 or
or  then
then and
and 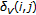 are randomly chosen in
are randomly chosen in 
 or
or  Then
Then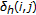 and
and  are randomly chosen in
are randomly chosen in 
 is chosen in
is chosen in 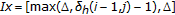 with a
with a is chosen in
is chosen in 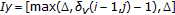 with a
with a and
and 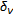 to the image size through
to the image size through do
do
 do
do
 Apply the displacement fields
Apply the displacement fields , read standard deviation
, read standard deviation  , read
, read 
 size of the low resolution displacement fields
size of the low resolution displacement fields 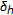 and
and 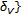
 and
and 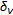 with random values in the interval
with random values in the interval 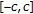
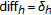
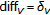
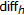 and
and  are
are  do
do

 do
do
 do
do
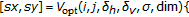 Find the optimum
Find the optimum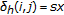


 and
and  to the image size through
to the image size through do
do
 do
do
 Apply the displacement fields
Apply the displacement fields , matrices of displacement fields
, matrices of displacement fields  and
and  ,
,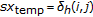

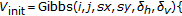 Initial potential
Initial potential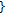
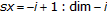 do
do
 do
do
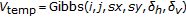
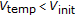 then
then

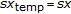
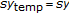

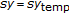
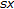 and
and 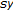
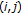 , displacements
, displacements 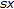 and
and 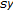 , matrices of
, matrices of
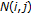 is a first order
is a first order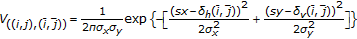
 , energy of the
, energy of the long message
long message middle
middle do
do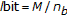
 and
and 
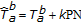

 in the zig-zag scan
in the zig-zag scan and load
and load middle
middle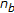 do
do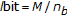
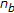 do
do , energy of the
, energy of the long message
long message
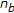 do
do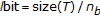
 and
and 

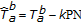
 , length of the watermark
, length of the watermark 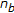 and load
and load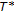
 do
do
 do
do